The Fall of Democracy is a Markov Process
Did you know that the Ancient Greek word "anacyclosis" translates to "Markov-chain Monte-Carlo"?
How do democracies die? With thunderous applause?
The ancient Greeks were, quite reasonably, concerned by this question, because their democracies died all the time. In fact, this happened so much that the most eminent philosophers and historians of the classical period developed a theory that rationalizes the rise and fall of democracies, oligarchies, and tyrannies. In this article, we will investigate whether their theory, called anacyclosis, holds up under scrutiny, and by scrutiny, I mean Monte Carlo simulations of government transition based on historical data from 1,035 Greek city states. But first, some history.
The Poleis of Ancient Greece
The peculiarities of classical Greece make empirical theories of political revolution much easier to imagine than in, say, the Persian Empire, which was a hereditary monarchy for pretty much its entire history. The dominant mode of social organization in the archaic and classical Greek periods is the polis, the city-state. Usually, there’s an independent mother city (Athens, Sparta, etc.) that politically, economically, and culturally dominates its surrounding hinterland. Each city has its own constitution, or form of government, but shares a common Greek culture and language with its neighboring poleis.
This social structure is as dynamic as it is unstable, and there were many political revolutions. The ancient world’s most sophisticated theories of political evolution grew out of this dynamic — they classify government into a few categories based on which group holds power, and posit that they devolve sequentially from higher to lower forms. Let’s take a quick look.
Governmental Types in Ancient Greek Thought
The Inventory of Archaic and Classical Greek Poleis, about which we will have much more to say later, gives a nice introduction to the types of constitution.
In Greek political theory politeiai [political institutions] were divided into types according to how many people constituted and manned the principal organs of government. Basically, there were three constitutional types: the rule of the one, the few and the many. Pindar is the first we know who distinguished between rule by a tyrant, or the wise, or the whole army. About a generation later, Herodotos has a debate about the three basic types of constitution, here described as demos, oligarchia and monarchia. [In the early 4th century BC], Plato called the three forms tyrannis, aristokratia and demokratia.
Linear Evolution in Plato’s Republic
Plato1 made a finer distinction, dividing government into five categories of constitution in his Republic, and additionally giving their sequence of devolution.
Aristocracy (rule by the best) → Timocracy (rule by honor/worth/money) → Oligarchy (rule by the few) → Democracy (rule by the people/mob) → Tyranny (rule by one man).
Plato writes that governments devolve in this order, from best to worst, in a linear fashion, terminating in tyranny. I went back and checked the Republic to see if he makes any claims of cyclical nature, and I don’t think that it does, but the Republic is very hard to read generally,2 so I’m not 100% sure.
Aristotle, a student of Plato, the tutor of Alexander the Great, and a giant of philosophy in his own right, generally agreed with Plato, but distinguished between a good and a bad form of monarchy (basileia versus tyrannis), minority rule (aristokratia versus oligarchia) and majority rule (politeia versus demokratia). His conception, however, was also linear (as best as I understand).
Anacyclosis in Polybius’ Histories
Polybius was a Greek hostage and historian in Rome during Rome’s rise to power, and he improved upon Plato and Aristotle’s framework. Polybius divided government into three categories, each with a virtuous and corrupt form, for a total of six constitutions. They are as follows, from his Histories:
The virtuous aristocracy is corrupted into an oligarchy, which is overthrown by the people as a democracy, which degenerates into mob-rule or ochlocracy. A great leader emerges from mob chaos to create a monarchy, which descends into tyranny before being overthrown by the noble aristocracy, beginning the cycle anew. He called this cycle anacyclosis.
The Anacyclosis Institute (to whom I must give credit for the genesis of this article)3, offers the following comments on this process.
There is good reason to think that Polybius and his predecessors arrived at this theory empirically. After observing the rise and fall of many hundreds of city-states, most of which cycled through several of the governmental forms mentioned above, Greek political thinkers concluded that these transitions from one form to another were not random. Rather, they seemed to follow simple and recognizable patterns. For example, tyrants were frequently overthrown by groups of aristocrats, while popular revolutions frequently overthrew oligarchies and ushered in democratic rule. Interestingly, the reverse of these trends (aristocracies being overthrown by tyrants or democracies turning into oligarchies) were statistically less likely to occur.
Through such observations, Polybius extrapolated the likely complete course of political evolution for an independent state whose lifecycle is not cut short by war or disaster.
Polybius, Plato, and Aristotle essentially agree on the pattern — we go from rule-by-few (aristocracy/oligarchy) to rule-by-many (democracy) to rule-by-one (monarchy/tyranny), with an optional cycle back to rule-by-few.4
Polybius thinks there’s a way out of this cycle. If one combines all three forms of goverment into a mixed constitution, a blend of democracy, aristocracy, and monarchy, one can create a stable system exempt from anacyclosis. Polybius thought that the Roman Republic was the embodiment of this mixed constitution and the reason for its strength and longevity. The Founding Fathers of the United States of America, and John Adams in particular, were obsessed with Polybius, and designed the structure of the United States government to avoid anacyclosis.
So to recap, we have several explicit claims, of which various authors claim subsets.
Political evolution follows a predictable pattern of oligarchy → democracy → monarchy
This pattern may be linear (Plato) or cyclical (Polybius)
The reverse transitions are unlikely/unnatural.
Unfortunately for Polybius, he lacked the tools to quantitatively investigate his theory. Fortunately for us, we are much better than Polybius at linear algebra.
Political Evolution is a Markov Process
Implicit in anacyclosis is actually a fourth claim, the most important claim, that anacyclosis is “memoryless.” In other words, the next type of government depends only on the current type of government: democracies always devolve to tyrannies, independent of what preceded democracy. In the theory of stochastic processes, this property is called the Markov property. We can use the Markov property to evaluate the validity of Polybius’ claim.
First though, we need data. Fortunately, the Copenhagen Polis Centre has done most of the work for us, and compiled An Inventory of Archaic and Classical Poleis,5 a monumental work that compiles the existing data/metadata on the 1,035 identifiable Greek city states of the Archaic and Classical periods (c.650-325 BC). Among the data found in the Inventory is a list of city states and their known government types, ordered by date.
This data is actually all we need in order to pretty fairly evaluate the validity of the theory! For each city state, we can simply extract ordered pairs of government types from this list, and count the frequency with which these transitions occur. Because anacyclosis is a Markov chain (remember that means memoryless), these transition frequencies completely define the system! Note that this method completely ignores staying in the same state as a transition of interest (that requires much more sophisticated data parsing). So this method will probe only when governments change between distinct types.
This will make more sense as we actually construct the transition matrix, and learn how to analyze Markov processes more generally.
An Introduction to Markov Processes through the Inventory of Greek Poleis
A Markov process, named after the Russian mathematician Andrey Markov, is a type of random process. It has discrete states and a notion of time. At each time-step in the process, each state X has a probability P(X→Y) of transitioning to state Y. The Markov (memoryless) property ensures that this probability is the only relevant characteristic of the system.
Markov processes are often represented by graphs that abstract these transition probabilities, like the one below from Wikipedia showing a two-state Markov process.

In essence, a Markov process is the simplest form of a probabilistic state-machine that still has interesting behavior. For any process that can be assumed to be stochastic, or perhaps a system complex enough that its behavior approximates a stochastic process, we can model it is a Markov process and immediately extract nontrivial, useful properties (as we shall see later).
Processes that (approximately) have the Markov property show up everywhere. Weather prediction, stock price prediction, and population genetics are all examples of approximately-Markov processes. In each of these cases, while the real system may have complex dependencies, a Markov model captures enough of the important behavior to be very useful while still being mathematically tractable.
So how would we construct a Markov model for political evolution in Greek poleis? Like any good scientists, the first thing we have to do is create a good visualization of our data, and stare at it.
The Data
Looking at our dataset, we have six distinct types of constitutions listed by the Inventory. I’ll quote briefly from it here.
In the Inventory, when we classify the constitution of a polis, we distinguish between basileia, tyrannis, oligarchia and demokratia, but we ignore variants of the two latter types, and all attestations of basileia belong in the Archaic period…
In a few cases of serious doubt, we have used Mix. to describe a polis with an unidentifiable mixture of characteristics.
The inventory also has another category in the data not listed above, politeia, which Aristotle defined as the “good” form of democracy, but is also the general term for a “polity” in Greek. Both of these last forms, politeia and “mixed” are very rare in the Inventory and slightly confusing.
We should note also that the Inventory says that the term basileia might change meaning over time, as it is only attested in the Archaic period and not the Classical period. Second, that “in actual fact, all polis constitutions were mixed,”6 to one degree or another.
But for a first cut, let’s ignore these complexities, and take a look at the data. First, the total frequency of government types:
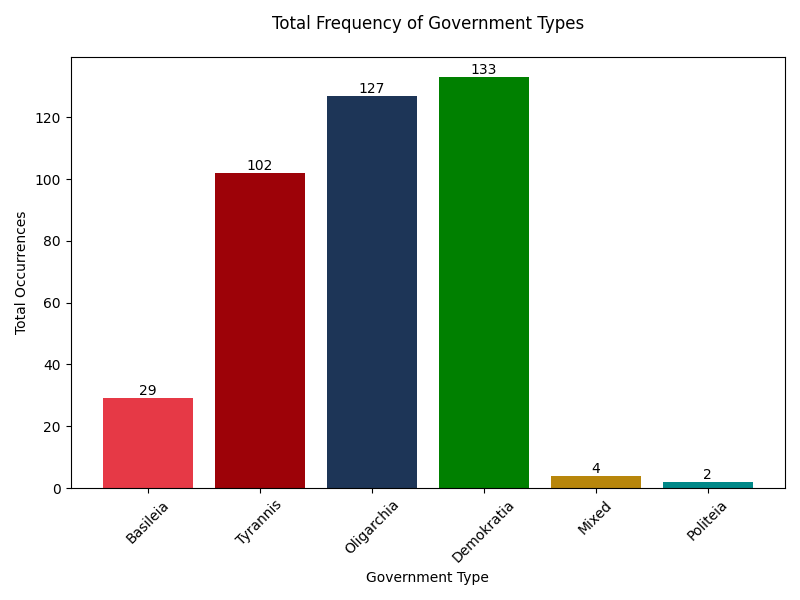
We note that the mixed and politeia types are very rare, and not likely to affect our results. Excellent! Let’s ignore them. Second, that if we combine basileia and tyrannis, the constitutions are roughly equal in frequency between the autocratic, oligarchic, and democratic categories. Interesting! We’ll keep the two types of monarchy separate for now.
Next, we can plot the frequency that any constitutional type appears first, or last. If Plato is correct, we would expect to see lots of oligarchies initially, and lots of tyrannies finally. We… might see some evidence for that? We really see more of a transfer between oligarchy and democracy from this graph, and the number of monarchies slightly decreases, but not a lot. I don’t think Plato gets much help from the data here.

Finally, we can plot the frequency of government transition type. We define this naively, taking the sequence of governments in the inventory, and plotting the frequency of each ordered pair, i.e. demokratia, oligarchia, basileia would could as one occurrence each of dem.→ol., ol.→bas..
This last plot is pretty much the key to Markov processes. We can simply reinterpret each column of the above heatmap as a probability of transition between states. Thus, by normalizing each column of the transition frequency heatmap, we get a transition matrix T that defines the process. Because our system has the Markov (memoryless) property, the single-step transition matrix entirely defines the process — it is a Markov process.
How does the model work in practice? Let’s enumerate the types of government as the ordered list:
[bas., tyr., ol., dem., mix., pol.]
Then we can define a one-hot vector v that corresponds to my state, e.g. [1, 0, 0, 0, 0, 0] = the system is in the basileia state. The probability of transitioning to any other state is then given by a vector p, equal to the the transition matrix T times v.
Let’s explicitly construct T for our data. Since “mixed” and politeia are ill-defined and occur so infrequently, I feel fairly justified in simply dropping those columns from the data.
From this matrix, we can then recreate the Markov-process-style node graph.
Assessing Validity
We’re now in a position to partially assess the validity of anacyclosis as it relates to the data, in a first-order sort of fashion.
The first claim is that political evolution proceeds in the order oligarchy → democracy → monarchy. Our data is fine-grained enough that we can split monarchy into its “virtuous” and “corrupt” forms, basileia and tyrannis, and so let’s look for oligarchy → democracy → basileia → tyrannis in the data.
Looking first at the basileia → tyrannis transition, we actually find excellent support for this in the data! Basileia to tyrannis transitions happen about 13 times more often than the reverse. However, there’s a confounding variable. Remember that the Inventory says that basileia is attested only in the Archaic period, so any basileia → tyrannis transitions might be the result of redefinition as opposed to transition. Let’s call this one a partial thumbs up, though.
How about the posited oligarchy → democracy transition? Not so much. These two nodes have the tightest connection in the graph, and the transition rates are essentially even, with oligarchy to democracy being ever so slightly more favorable than the reverse.
Finally, what about democracy → monarchy? It seems as though democracies don’t ever go to basileiai, which certainly doesn’t support the theory of anacyclosis, but again, this could be a definition thing — if we started the chain at basileia, we could have passed through the Archaic period before we got back around, when basileiai had turned into tyrannides. Unfortunately though, the democracy → tyranny transition (29%) is much less common than tyranny → democracy (56%). This gets even worse if we consider basileia the same thing as tyrannis, which has even more asymmetry between the two transition frequencies. So the democracy to monarchy transition doesn’t find much support here, in fact, more the reverse.
In fact, what is the most common cycle? Let’s re-plot the Markov chain where we combine tyrannis and basileia into “monarchy.”
This doesn’t really help us much. The most plausible cycle by far is simply oscillation between democracy and oligarchy, which does not at all fit into the anacyclosis paradigm. It seems we require a more sophisticated analysis to extract the probable dynamics.
Markov Chain Monte Carlo
Okay, well then what does happen to a hypothetical average Greek polis? We can use a Monte-Carlo style simulation to find out.
“Monte Carlo” is a cute name for a very simple technique — if you have the rules of a system and want to understand its behavior, just simulate a whole bunch of random instances of that system and average the results. The simulation method is called “Monte Carlo” because one of the inventors had an uncle who gambled too much in real Monte Carlo.
Nevertheless, this simple technique is extremely powerful. To implement, we
Choose an initial one-hot state v
Multiply by our transition matrix to get p = Tv, our vector of state probabilities
Choose a random state from p, weighted by the probabilities of each state, i.e. if p = [0.1, 0.2, 0.3, 0.4], we have a 10%, 20%, 30%, and 40% probability, respectively, of choosing states 1, 2, 3, 4.
Repeat this for n timesteps
Repeat steps 1-4 for m simulations
Let’s try this out, keeping the basileia/tyrannis distinction, just for fun.

So keeping basileia as a separate category doesn’t do much, its occupancy fraction immediately hits zero (on average) and never recovers. The most distinct feature by far appears to be the oligarchy-democracy oscillation, settling after 10 timesteps into an even mixture of democracy and oligarchy (remember this is an average, at each timestep, the system can only be in one state). The tyrannis initialization appears to cause the settling to happen faster, but doesn’t differ in the essential trend. We also appear to stabilize at a steady state for any initialization parameter! Perhaps this is the fabled “mixed” constitution that Polybius thought made the Roman state so powerful and stable? We shall formalize this thought later.
Before we do steady-state analysis, we should check for common cycles. Let’s plot the most common cycles we find, dropping the basileia/tyrannis distinction (both are monarchy) for clarity. 1000 more simulations…
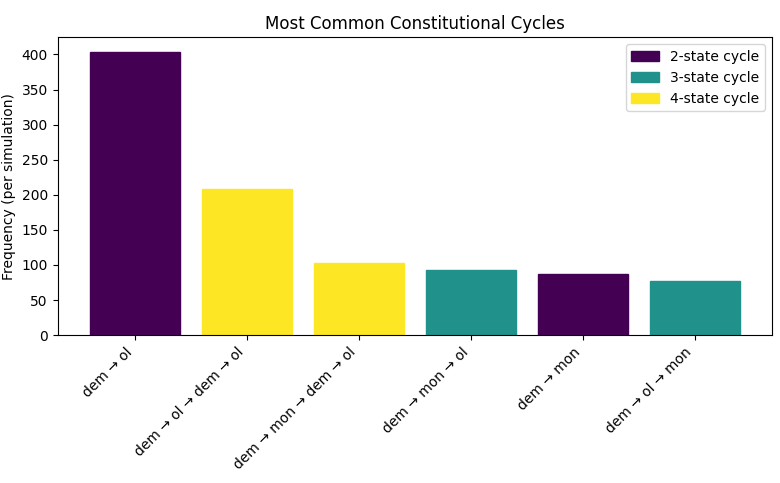
The most common cycle by far is the 2-state democracy → oligarchy → democracy cycle. The next most common state is this same cycle, twice in a row!
But wait, if we look down the list at the fourth most common cycle, it’s democracy → monarchy → oligarchy → democracy, that’s anacyclosis! It is the most common 3-state cycle! We found it!
Did we just prove anacyclosis is real? Well, uh, it depends what you mean, I guess.
Instead of answering the above, difficult question, I choose to reinterpret the original theory in light of the data — when Polybius wrote that “anacyclosis consists of predictable, cyclic transitions from democracy → monarchy→ oligarchy,” he clearly must have meant that given the empirical transition probabilities derived from a Markov model of Greek city state constitutional data, a Monte Carlo simulation will show the most common three-state cycle is democracy → monarchy → oligarchy.
I think this is a very reasonable translation of the original Ancient Greek.
Mixed States and the Stable Distribution
Now Polybius was particularly interested in ways out of this endless cycle. How can we find a stable governmental state? Both our answer and Polybius’ answer is the same, and is already hinted at by the results of the simulations. We noted earlier that the simulations, regardless of initialization state, seemed to settle into a predictable distribution of government types, roughly 40% oligarchy, 40% democracy, and 20% tyranny. This was also Polybius’ answer, that a mixed state was a stable point of this Markov process.
Polybius took as his example par excellence the constitution of the Roman Republic, which had popular assemblies (democracy), the Senate (oligarchy), and two consuls with executive power (a dash of monarchy). He felt that this mixture was much more stable than any pure state, and lent Rome its fabulous power.
According to our model, Polybius is absolutely correct.

How can we find the stable state of our Markov process? Well first, we extend the model to allow for mixed states by not forcing our state v to be one-hot. That’s fairly easy. But how do we find the long-term stable state, if there is one?
Let’s think geometrically about our transition matrix. For a 2 × 2 transition matrix, we can visualize its action by seeing how it transforms a set of vectors arranged along the unit circle in the plane.
Under this linear transformation, the unit circle becomes an ellipse. The special directions that remain unchanged (up to scaling) by this transformation are called eigenvectors. These are precisely the principal axes of the resulting ellipse.
Mathematically, an eigenvector v with eigenvalue λ is defined by the equation:
where T is our transition matrix. But this is very helpful for us, because if I now apply T twice, I get
Thus when we apply T repeatedly, each application multiplies the magnitude of v by λ while preserving its direction.
This means:
If λ = 1, v maintains its magnitude: it's a stable state
If |λ| > 1, v grows without bound
If |λ| < 1, v shrinks toward zero
For Markov transition matrices, the Perron-Frobenius theorem guarantees that 1 is always an eigenvalue, and all other eigenvalues have absolute value strictly less than 1, meaning they decay to zero after a long time. When the Markov chain is also ergodic, meaning that you can visit any state from any other state, and you never get stuck in deterministic cycles, this unit-eigenvalue direction corresponds to a unique stable distribution called the stationary distribution.
Any initial distribution will converge to this stationary distribution as we repeatedly apply the transition matrix. We actually saw this in our Monte Carlo simulations — did you notice how, no matter the initial state, we always ended up with the same fraction of oligarchy/democracy/monarchy?
So we can quite quickly find the stationary distribution of our transition matrix by performing an eigendecomposition of our transition matrix. We solve
for all v and λ.
Let’s take our transition matrix where we combine basileia and tyrannis into monarchy.
The eigendecomposition of T yields three eigenvectors.
Which does indeed have a unit-valued eigenvector! To find the stationary distribution, we only need to normalize the eigenvector with eigenvalue 1, by dividing it by its column sum (it’s a probability vector, remember).
We can visualize this final distribution with a bar graph. Bar graphs are the most useless graph type, but they are visually arresting due to large bars of solid primary colors, so I’m making one.

This graph shows the anacyclotically stable distribution of the Markov poleis model. I don’t know if the word anacyclotically will ever really catch on in popular discourse, but I think it really rolls off the tongue. Perhaps instead we should call it the Polybian distribution. It does look remarkably similar to the Roman system, which was deeply suspicious of kingship, but recognized its utility, and hence had two equal consuls in the place of one tyrant, as well as theoretically balanced popular assemblies and an aristocratic/oligarchic Senate.
So that’s it! This is the final confirmation that Polybius was on the right track, and that if he had only been better at linear algebra, he could have quantitatively estimated the proportion of democracy, monarchy, and oligarchy to inject into a politeia to stabilize it against the inevitable anacyclosis, assuming of course that by anacyclosis he actually meant the stochastic Markov process we’ve been working with this whole time, and not the actual anacyclosis that he wrote down, which is given minimal support by the actual data. Easy!
I should note, for future work, that there is at least one major oversight — for any given year in even the most fractious Greek polis, the probability of government transitioning to an entirely new category is small. In other words, I could have structured this process around a timestep being a single year, instead of an arbitrary “government transition time,” and gotten very different looking processes, with the same long-run transition probabilities. Oh well, you always have to leave work for the next researcher.
Addendum: Methodological Validity
Mere minutes after posting this article, I had a thought — is the Greek poleis data set even capable of detecting an anacyclosis cycle in principle?
Let’s say I have a sequence A → B → C → A → …, like our poleis dataset. Then, because of spotty recordkeeping, let’s say I decimate this sample by randomly deleting entries, so maybe I’d get A → B → __ → A → …. Without knowledge of the original sample, there’s a spurious B → A transition in our data!
So the question I want to ask here is, given a sequence composed of a pure cycle S = A → B → C → A …, if I randomly sample this sequence by throwing away all but a fraction f of the data points, can I still detect my sequence above noise?
Formally, let’s ask the question in the following way: I sample a fraction f of the data points from my sequence S, and construct a Markov transition matrix T by naively measuring transition frequency between neighbors in my sampled sequence. How often will I measure that the probability of the original sequence is greater than that of the reverse sequence? This is a sensible definition of “noise” because if we are solely interested in three-element sequences with unique elements, there are exactly two, A→B→C and C→B→A.
This sounds like an interesting analytical problem, but keeping with the Monte Carlo theme of this article and my own laziness, let’s just try it in code. I’ll construct a sequence of length 100 (A→B→C→…), decimate it, keeping a fraction f of the data, construct my matrix T, and then check whether the original cycle probability exceeds the reverse cycle probability.
The results are as follows.7

And for completeness, does this give sensible results when run it on the reverse sequence C → B → A? In other words, what’s the spurious detection rate for a sequence that doesn’t contain the cycle at all?

Yes. This test does indeed give sensible results.
How about a random sequence? What do we expect on average?
Yes, this also makes sense. For a random sequence, we detect that A→B→C is more probable than the reverse about 50% of the time. I think this is a “type III” error, where I correctly detect that the probability of my sequence is higher than the reverse sequence (the noise), but this doesn’t mean anything, because the underlying generator is fully random.
Based on this, I think I can say that the cutoff point where this detection mechanism starts to work is when the probability of detection exceeds ~50% on that curve, so let’s say a sampling fraction of about f = 0.2. That’s not too bad, I think I can consider my method valid enough for a substack article.8
Whose name means “broad,” by the way. It was his wrestling nickname, not his given name.
And filled with bad advice, in my opinion. Plato is a lot like Marx, I think — brilliant diagnosis, terrible prescription.
And credit especially to Lantern Jack of the Ancient Greece Declassified podcast, who introduced me to the concept, and to An Inventory of Archaic and Classical Poleis
I note that the political revolution in Star Wars, when Emperor Palpatine usurps the authority of the Galactic Senate, accurately follows the principles of anacyclosis, though Polybius says nothing about thunderous applause.
PDF link here, thanks again to Lantern Jack’s Ancient Greece Declassified podcast for showing me that this existed.
Inventory of Archaic and Classical Poleis, page 84.
I’m using the Wilson confidence interval here, because a standard confidence interval gives detection fractions greater than 1, and Wilson intervals are appropriate for binomial-like scenarios like “I detect” or “I do not detect” according to ChatGPT. I think this makes sense.
Unfortunately, I think a real-time-aware method wouldn’t have this problem at all, because a gap in the data would show up in the dates that the constitutions are recorded… I probably should have done that, but it’s a LOT more work.











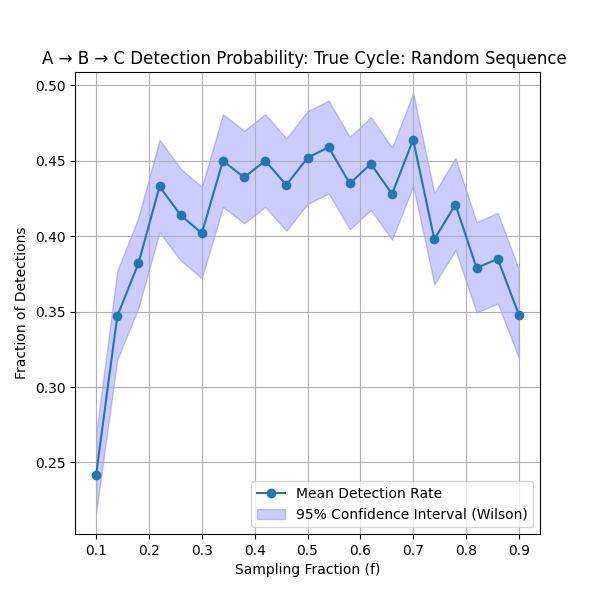
Amazing, although the conclusion of "American-style governance is provably the most stable" would have rang less hollow ~10 years ago.
As a person whose so is an economist modeling this kind of stuff seriously, I am impressed