Guinea Pigs are Fermions -- Part 1
Part 1 of a series exploring the quantum mechanics of guinea pigs, with a short digression into creation and annihilation operators and their uses in guinea pig quantum mechanics.
What is a Guinea Pig?
A guinea pig is a small, pear-shaped rodent whose main ambition in life is to consume huge quantities of fresh produce and timothy hay.
Guinea pigs in the wild often reside inside of a little plastic igloo, called a pigloo.
Guinea pigs in pigloos exhibit fascinating confinement properties. A pigloo can hold at most two guinea pigs at any one time, and when two guinea pigs simultaneously occupy a pigloo, the guinea pigs are always anti-aligned.
Guinea pigs naturally obey the Pauli Exclusion Principle, which states:
The Pauli exclusion principle states that two or more identical particles with half-integer spins (i.e. fermions) cannot occupy the same quantum state within a quantum system simultaneously.
More simply, no two fermions (of which electrons and protons are the most common examples) can ever be in the same state. In fact, the Pauli Exclusion Principle is the defining characteristic of fermions! Since guinea pigs in pigloos exhibit precisely this property, we therefore conclude that guinea pigs must be fermions. My father, who originally formulated the Piggy Exclusion Principle, postulated that guinea pigs, like fermions, must have half-integer spin, which he called pigspin.
The Quantum Mechanics of Fermions (And Guinea Pigs)
Since guinea pigs are obviously fermionic in nature, with half-integer pigspin, we can use all the machinery of quantum mechanics to describe the dynamics of guinea pigs in pigloos.
Quantum mechanics is a famously difficult subject to understand, so in this article I’m going to try to sketch the mathematical concepts without too much detour into operator theory and Hilbert spaces. That being said, in order to construct the guinea pig Hamiltonian, let’s first discuss the Schrodinger equation.
The Schrodinger Equation
This is the Schrodinger equation, the most famous equation of quantum mechanics.
The Schrodinger equation relates the time-evolution of the wavefunction ψ to this mysterious quantity Hψ.
ψ is the wavefunction, a function which in some way contains everything we know about a quantum object, its position, its momentum, its charge, etc.
H is an operator called the Hamiltonian, a function which acts on ψ.
For our purposes, the Hamiltonian operator can be thought of as the total energy of the system. That is, when H acts on ψ, it produces the total energy of the wavefunction times the wavefunction.
The first, and most important, step in solving a quantum problem is coming up with a good Hamiltonian operator that describes your system. In order to do that for our problem though, we first need to understand a little bit about operators, and a little bit of Dirac notation.
Dirac Notation, Creation and Annihilation Operators
Dirac notation, also called bra-ket notation, is a very convenient mathematical notation for keeping track of vectors with complex elements, and so let’s briefly introduce it.
Kets
This is a ket:
A ket represents a column vector with an arbitrary number of elements, and a label, in this case ψ.
Bras
This is a bra:
A bra is a row vector whose elements are the complex conjugates of the corresponding ket. In other words, a bra is the complex transpose of the ket.
Bra-kets and dot products
When you put a bra and a ket together, you get a bracket! It represents the dot product between the two vectors (with a complex conjugate).
Finally, it’s important to remember that the label inside of the bra/ket is just that, a label. It represents a vector. Honestly, that’s kind of all you need to know about Dirac notation. It’s really useful.
Creation and Annihilation Operators
If quantum states are represented by vectors, then operators are simply matrices. Any symbol with a little hat is going to be a matrix.
Creation and annihilation operators, or ladder operators, are special matrices that act in a very useful way on specific quantum states. They’re best thought of as moving a particle state with |n> quanta (a quanta can be a unit of energy, or a particle, or a unit of momentum, whatever) up and down a ladder, where each rung on the ladder is a state with different number of quanta. Think energy levels, and |0> is the ground state. Remember, the number n in |n> is just a label. It does not necessarily imply anything about the vector representation of |n>.
Each time the that a state with n quanta |n> is acted upon by the creation operator a_dagger, a new state with n+1 quanta is produced. When a state |n> is acted upon by the annihilation operator a, the state |n-1> is produced.
When the “end” of the ladder is reached, we produce 0:
Try not to overthink this picture, and for now just think of this as rules for pure symbol manipulation. However, remembering that these operators a and a_dagger refer to actual matrices, remember that the dagger superscript means “complex transpose,” the same as for vectors.
Commutation Relations
These ladder operators are further defined by their commutation relations, which has a lot of deep physical meaning that I’m going to totally skip in favor of a matrix-based explanation.
Given two real numbers, a and b, these two numbers commute, i.e. it doesn’t matter in which order they’re multiplied.
Let’s write this differently, in terms of the commutator brackets.
However, two matrices A and B do not necessarily commute.
The commutator brackets “measure” how non-commutative two matrices are. The more commutative they are, the lower the commutator, and the more number-like they behave.
Since creation and annihilation operators are matrices, they don’t necessarily commute either. Given a set of annihilation operators a_i that act on different things (lattice sites, pigloos, etc.), labeled by an index i:
The commutation relations of bosonic ladder operators are given by:
Fermionic ladder operators instead obey anti-commutation relations (AB + BA instead of AB - BA) ,
The Anti-Commutation Relations of Fermions Imply the Pauli Exclusion Principle.
Okay, now that we’ve learned a bunch of meaningless symbol manipulation, let’s connect it to something physical.
Let’s say we have a system with two potential states, ↑ and ↓. You can think of these as orientations of guinea pigs in a pigloo, or electron spins, whichever you prefer. Let’s define two creation operators that create, respectively, ↑ and ↓ guinea pigs.
Starting from the vacuum state |0>, we now create a state with two pigs. We’ll do it in two ways:
Let’s sum these two equations.
Because we have defined these two operators to anticommute, we have
Or more simply:
We see that fermions are antisymmetric under interchange of particles/guinea pigs. If we switch the up pig and the down pig, our state must gain a negative sign.
However, if the two guinea pigs are in the same state, we have
No two piggyons can be in the same state! The anticommutation relations imply the Pauli exclusion principle.
The number operator
I’m not going to explain this one too much, but it’s also important to know that the product of a creation and annihilation operator is called a number operator, and has this special property when acting on so-called “number states”
The number operator counts how many quanta are in a number state.
The Single Pigloo Hamiltonian
Okay, after that long digression into terminology, we are in a position to write down the full guinea pig Hamiltonian!
Let’s consider all the possible states of a single pigloo.
What is the total energy of each state? Let’s assume that each pig carries one quantum of energy E. Let’s also assume assume that putting two pigs in the same pigloo raises the energy of that pigloo by an additional interaction energy U. This is sensible, as guinea pigs don’t really like having to share a pigloo.
Remember, the number operator counts the number of pigs in a particular state. Since these pigs are fermions, the number operator will produce only 0 or 1, which makes this particularly easy. Let’s count the energy in each of the four possible pig states.
Multiple Pigloos and Pigloo Hopping
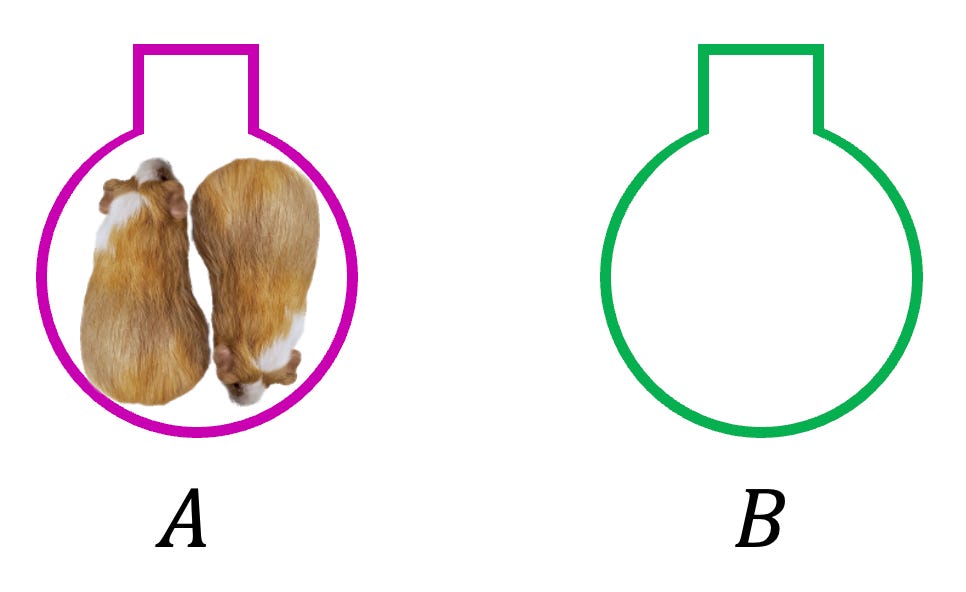
Let’s now consider a system of two pigloos, A and B, each with some number of guinea pigs.
What’s the total energy of this system? Without interaction between pigloos, it is simply the sum of the energies of the individual pigloos.
Here we sum over both pigspins and both pigloos. This system is precisely equivalent to adding two pigloos together, and is thus not very interesting.
However, with two pigloos, there is a new possibility that arises from their interaction! A guinea pig can hop from one pigloo to an adjacent pigloo. How can we add this to our Hamiltonian?
The standard method of writing transitions into a Hamiltonian is to “destroy” a particle in the start state and “create” a particle in the end state. For example, the transition above where the down pig hops from A to B would be written as
I also gave this term a weight -t. This is conventional for “tunneling events.” In quantum mechanics, tunneling is a mysterious phenomenon with no classical analogue where particles can move through barriers that wouldn’t be penetrable classically. With guinea pigs, tunneling events are often into the litter, or into the hay.
Let’s now sum over all possible transitions (to adjacent pigloos).
And there we have it! This expression captures the essential dynamics of fermionic guinea pigs hiding in pigloos, and has a surprising amount of mathematical depth.
I’ve intentionally written this Hamiltonian to be valid for N pigloos, not just two. It also happens to be the exact same Hamiltonian as the Hubbard Model, one of the simplest and most useful quantum mechanical models in solid state physics.
The Hubbard model is easy to understand and simple to write down, but mathematically rich. It contains the essence of complex collective phenomena in a simple Hamiltonian, such as metal-insulator phase transitions, and a modification called the t-J model is used to model high-temperature superconductivity. And, as it turns out, models the dynamics of guinea pigs.
I think this post is sufficiently long already, and so I’ve broken it up. In part 2, we will analytically solve the two-pigloo model and explore its dynamics. Then, we’ll move into more complex lattices of pigloos, and if we’re lucky, simulate a pig density wave!
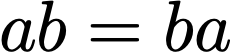
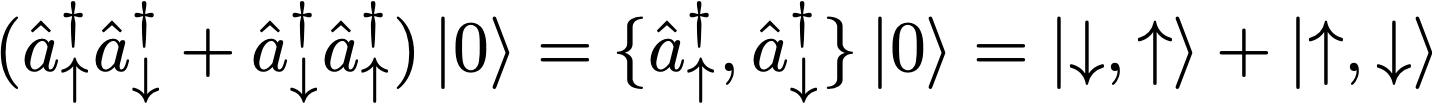
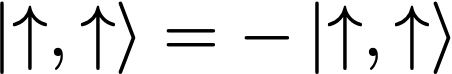
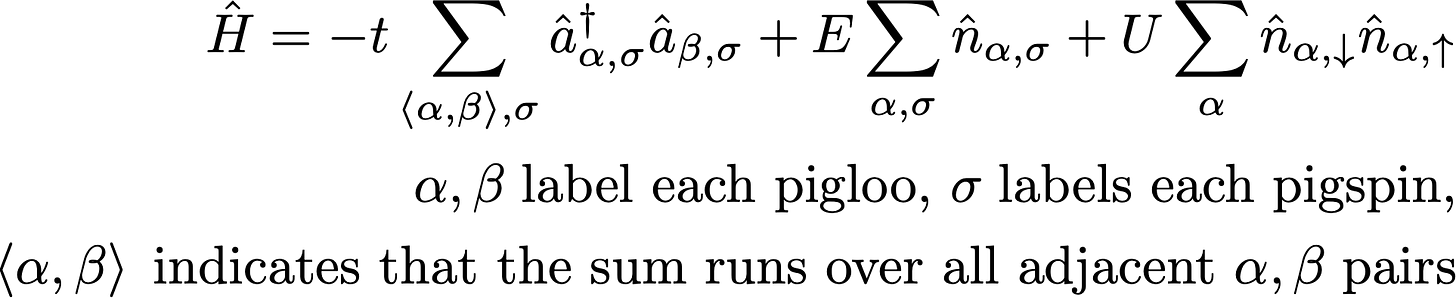
The spot where this lost me a tad is when you introduced a_hat_dagger. An explanation of that meant would have been helpful. I was thinking of them as separate (dagger == jump up a state, hat == jump down a state). But it wasn’t explained exactly what it means for the a vector to have both symbols so I was left to guess. Any help with what they mean?