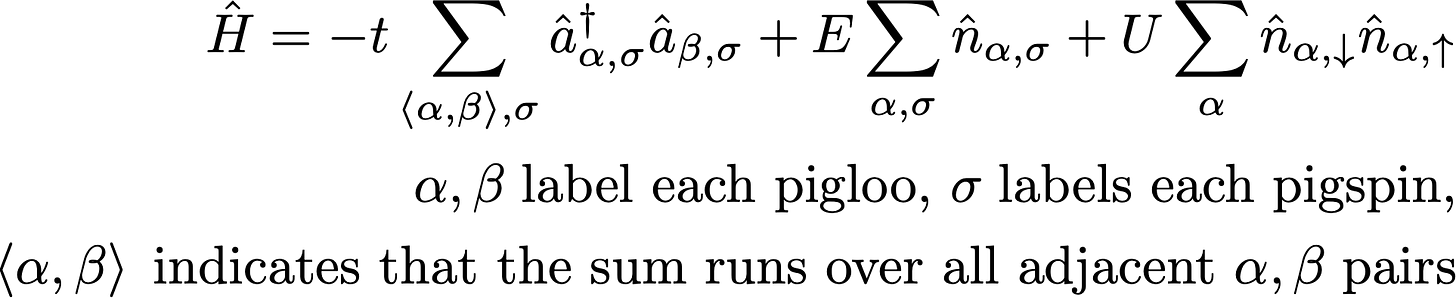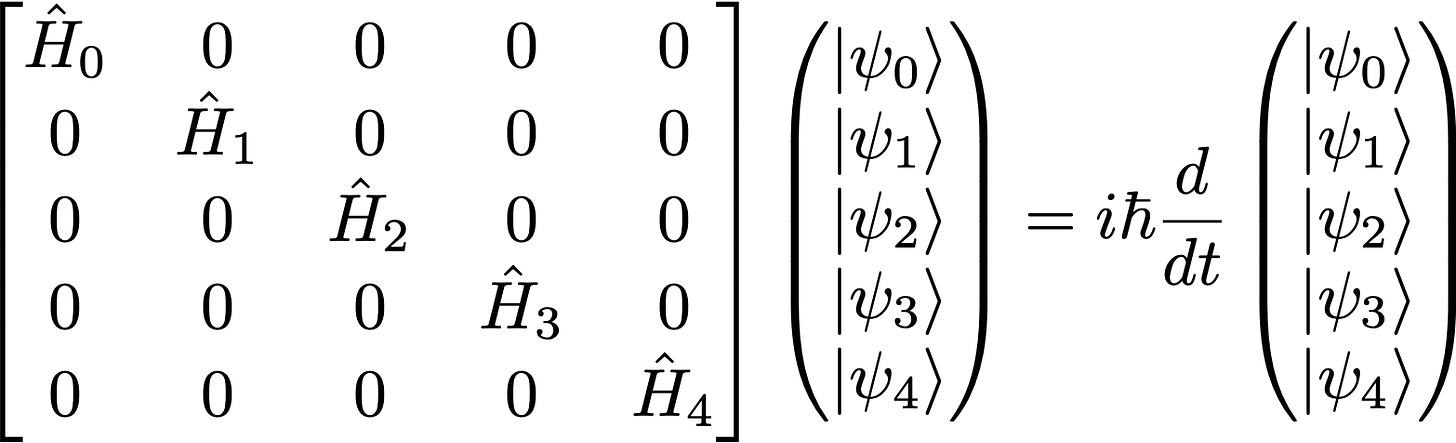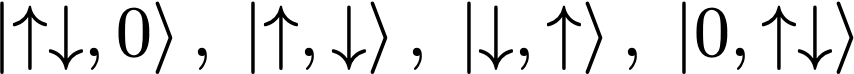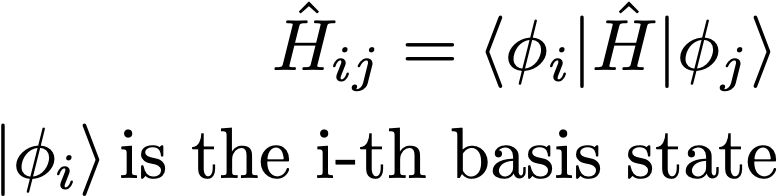Guinea Pigs are Fermions -- Part 2
In part 2 of our series, we analytically solve the two-pigloo model, simulate an 8-pigloo lattice to observe pig density waves, and discuss the utility of universal guinea pig quantum computation.
This post is part 2 in a series about the quantum mechanics of guinea pigs. You can read Part 1 here:
A Quick Recap of the Hubbard-Demelza Model
Last time, we derived a model for the dynamics of fermionic guinea pigs in pigloos, and I began to really wish that Substack supported LaTeX.
In this model, we have three terms. The first term is known as the “hopping” or “tunneling” term, and describes a pig hopping from pigloo β to pigloo α, while preserving its spin σ. The second term is the self-energy term, and counts the number of pigs, yielding a quantum of energy E for each pig, regardless of state. The third term is the interaction term, which adds an additional energy when two pigs share a pigloo. Pigs generally don’t like sharing pigloos.
In honor of John Hubbard, who first derived this Hamiltonian for solid-state physics and of Demelza, the friendliest guinea pig ever, we’re going to name our Hamiltonian the Hubbard-Demelza model, and solve it exactly in the case of two pigloos. We’ll simulate some more guinea pig dynamics in larger pigloo lattices, but the two-pigloo case is of fundamental importance, because my parents’ guinea pigs have two pigloos.
Simplification in the Pigloo Dimer Case
First we’re going to simplify the Hamiltonian a little bit. You see, that second term in the Hamiltonian that simply counts the quanta of energy for each pig, and captures no interactions between pigs or between pigloos. It’s not a very interesting term, and in fact only causes a constant energy shift without affecting the pig dynamics.
So let’s cross off that second term, and write out the Hamiltonian explicitly for the two-pigloo case, which we’ll call a Hubbard-Demelza Dimer.
This Hamiltonian is actually quite simple. Assuming all guinea pigs are in the ground state and not excited (no fresh produce), there are 4 states per pigloo, and 2 pigloos, giving us 4^2, or 16 total states. I’m not going to enumerate them, but imagine all sixteen of them watching you with their beady little eyes.
Remember that the Schrodinger equation (our goal) is a matrix equation, and we’ve just constructed an abstract representation of our 16x16 Hamiltonian matrix. Now we need the explicit matrix form.
Since we have sixteen total states (our Hilbert space has dimension 16), our Hamiltonian matrix is 16x16, which is pretty large. Fortunately for us, the Demelza-Hubbard model can be partitioned into much smaller, easier to handle subspaces.
Conservation of Pigs
The Demelza-Hubbard model has no term for generating guinea pigs ex vacuo, nor for destroying them.
Consider five sub-cases of our problem, containing, respectively, 0, 1, 2, 3, and 4 guinea pigs. Conservation of pigs implies that the Hamiltonian matrix has no transition elements that couple these subspaces. Thus, our Hamiltonian is block-diagonal, and the pig number states can be treated as evolving separately.
Conservation of pigspin
Each pig has a pigspin of +1/2, an up-pig, or -1/2, a down pig. Our Hubbard-Demelza Hamiltonian has no terms which correspond to spin-flipping — an up-pig remains an up-pig when hopping pigloos. This means the total pigspin S_z is also conserved, and we can partition the Hamiltonian by total pigspin as well.
Subspace partitions
The following table lists all the independent subspaces, and numbers the pig states allowed by the Pauli Exclusion Principle in each state.
Each of these nine subspaces may be solved separately.
Exact Solutions to the Half-Filled Dimer
Let’s look at the largest subspace, the 2-pig, 0-pigspin subspace containing one up pig and one down pig.
Here are the possible states:
A general vector in our system will be represented by
If we apply our Hamiltonian to these basis states, we can explicitly construct its matrix form. The procedure is a bit involved, and is left as an exercise for the reader, but here’s the answer:
Let’s first look at the energy spectrum. The eigenenergies and eigenstates of the system (the stable states and their energies), can be found by diagonalizing the Hamiltonian, and this gives us:
Now what are these states? Roughly, these are the stable states of the system, the ones in which the guinea pigs remain stationary, i.e. the pigloo occupation does not change with time.
For example, consider the first state:
This even superposition of singly occupied pigloos is a stable state. A guinea pig thus prepared will remain in this state indefinitely. It also happens to have zero net energy.
The energies of the other states are not so simple, and are controlled sensitively by the ratio of U to t, called k = U/t here. When U » t, the pig-pig interaction dominates, and when U « t, the pig-tunneling behavior dominates.
As you can see, when U/t → infinity, we have ω+ → infinity, and ω- → 0. We see the blue & green and red & orange states become degenerate, and the singly-occupied pigloos become highly favorable. This is also known as the highly-correlated limit.
By contrast, when U/t → 0, pig hopping energy dominates, the blue & orange states converge, and we have three classes of nondegenerate states. This is known as the tight-binding limit, where guinea pigs are tightly bound to their individual pigloos.
Two-Pigloo Dynamics
We can now solve the Schrodinger Equation by direct integration, and look at its dynamics.
Let’s prepare our system with in an initial condition that is not a stable state, so that we can see how the pig states evolve with time. I’ll choose U = t = 1, an equal balance of pig hopping and interaction energy.
The evolution of the pig states is then given by the solution to the Schrodinger equation above. Here, we plot the probability of finding the pigs in a given state vs. time.
Notice that if we prepare the pigs in the initial state |↑↓,0>, after about 6 units of time, the pigs will be found, with 100% probability, in the state |0,↑↓>. This is a coherent transfer of two pigs between pigloos. Cool!
We can compare the highly correlated limit to the tight binding limit, and see the differences:
The highly-correlated limit behaves as an effective two-state system, and we can excite guinea pig Rabi oscillations. The tight-binding limit shows similar, more complex oscillations involving all four states.
Simulations of N-pigloo systems
The two state model is very cool, and gives us a really good idea of how to control pig dynamics in simple systems. Larger systems become computationally intractable quite quickly, but we can look at an 8-pigloo lattice pretty easily.
Disclaimer: It’s about here that my expertise ends. We’re moving into computational quantum mechanics with nontrivial problems. I am fairly sure I did the following simulation right, but who knows?
Let’s simulate what happens in an 8-pigloo lattice when you initialize four guinea pigs into it. In an attempt to reduce errors, I’m going to use the OpenFermion package from Google, and modify their Hubbard Model Notebook for guinea pig dynamics.
Here is the Google Colab code I’m using.
Half-Filling of 8-pigloo 1D lattice
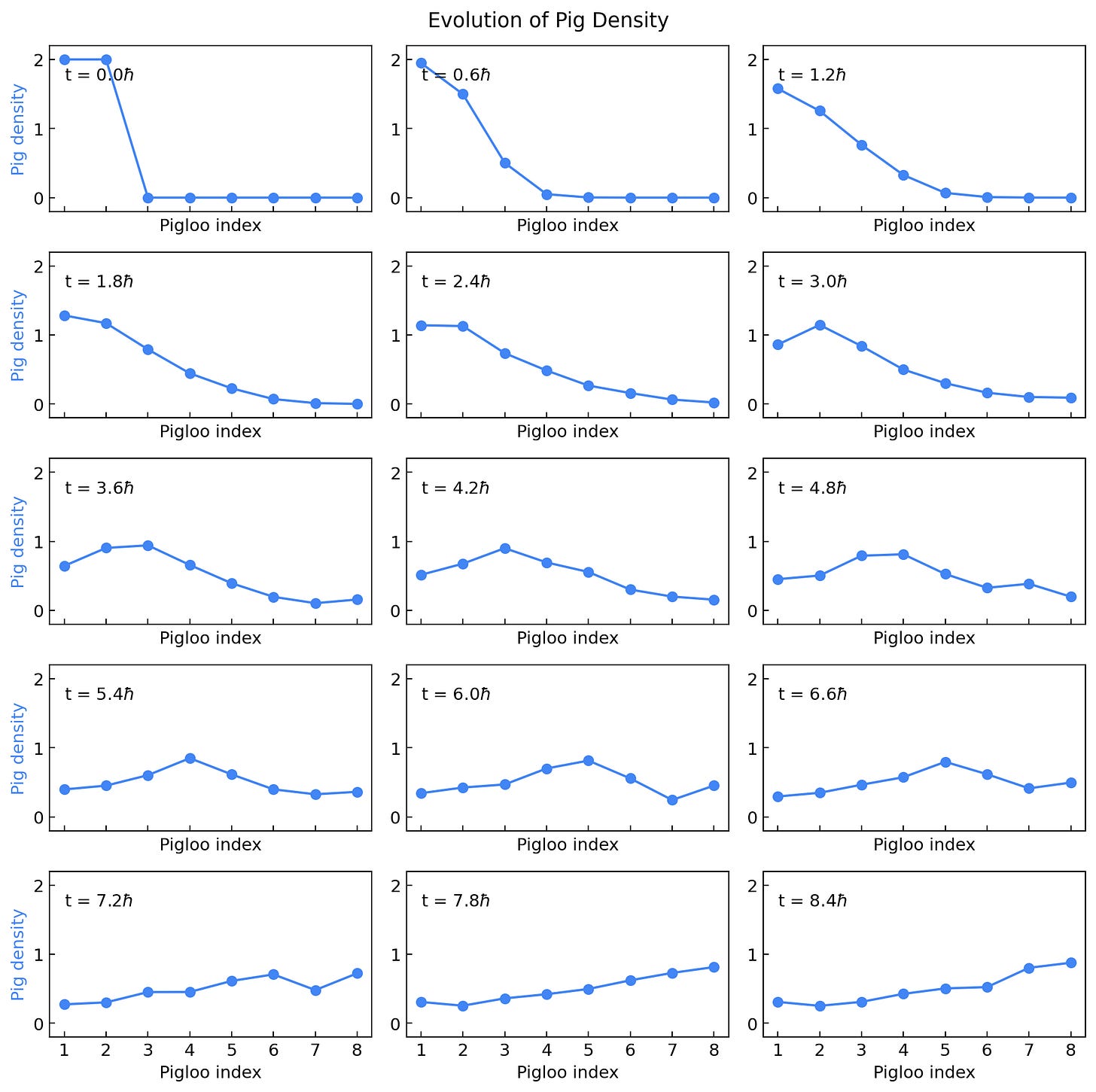
Okay, so let’s take the 8-pigloo lattice (8 adjacent pigloos) and initialize them with four pigs, two up and two down, in the first two pigloos. I’m using the Hartree-Fock method of initialization from OpenFermion, which, if I’m being honest, I do not fully understand. However, the state is going to look something like this:
As you can see, the pig density (the expectation values of the number operators for up and down pigs) shows two pigs in each of the first two sites. Due to the Pauli Exclusion principle, the two pigs in each pigloo have opposite pigspin.
Now, using a Trotterization method where we split the Hamiltonian up into parts, evolve each part separately, then multiply their propagators, we can simulate the evolution of the pig density. I’m using t = 1, U = 2 here.
The following figure plots the pig density over time, reading left-to-right, top-to-bottom.
As you can see, the initial concentration of pigs in the left-most pigloos spreads over time to become a more uniform distribution of pigs, but it does so as a wave of pigs traveling through the lattice, eventually breaking on the right-most edge of the lattice. This behavior agrees well with experiments conducted in the lab, though sometimes the particles get scared, run off, and have to be lured back with treats.
The Most Important Question
So that’s it! This is the culmination of our foray into quantum dynamics of guinea pigs. We’ve explored the consequences of the fermionic nature of guinea pigs, analytically solved the important pigloo dimer case, and simulated a probability wave of guinea pigs as they spread themselves out among adjacent pigloos.
We’re finally in a position to ask the most important question of all. Can we make a quantum computer from guinea pigs?
Simplifying a bit, universal quantum computation requires 4 elements. If guinea pigs can do all of them, we can make a quantum computer out of them.
1. A Qubit
A qubit is simply a two-level quantum system. You must have a way to represent 0, 1, and any arbitrary superposition of the two.
This is trivial with guinea pigs. We could use their pigspin degree of freedom, for example, with up-pigs representing 0 and down-pigs representing 1.
We could also use a dual-rail encoding scheme, where we label one pigloo ‘0’, and another pigloo ‘1’, and the qubit is encoded by whichever pigloo contains a guinea pig.
2. Single-Qubit Gates
We must be able to manipulate the quantum state of a single pig. Again, this is trivial with guinea pigs, as they’re relatively easy to catch, having very short legs.
3. Two-Qubit Gates
This one is tricky. We need to generate entanglement between guinea pigs for quantum computation. Entanglement is a much-mythologized property of quantum mechanics, where two independent single-particle states become a single, indivisible dual-particle state. This is where all the power of quantum computing comes from!
The simplest way to do this with guinea pigs would be to find some sort of guinea pig beamsplitter and interfere pigs. I am not currently sure how to do this, but it’s an active area of research. Presumably, some form of guinea pig obstacle course with multiple inlets and outlets would do the job.
Larger lattices of such guinea pig interferometers could be used for Bell state preparation.
4. Measurement
Finally, we need some way to read out the guinea pig state with high fidelity. Naturally, disturbing the guinea pigs alters their state, and so this is also quite tricky. Fortunately, the advent of camera phones makes it quite easy to photograph unsuspecting guinea pigs.
In conclusion, yes, it is possible to build a quantum computer with guinea pigs, indeed, it is a much more promising approach than several current approaches to quantum computing! However, given the need of ~millions of qubits for a useful simulation, the overhead in hay and lettuce would make such a computer prohibitively expensive.