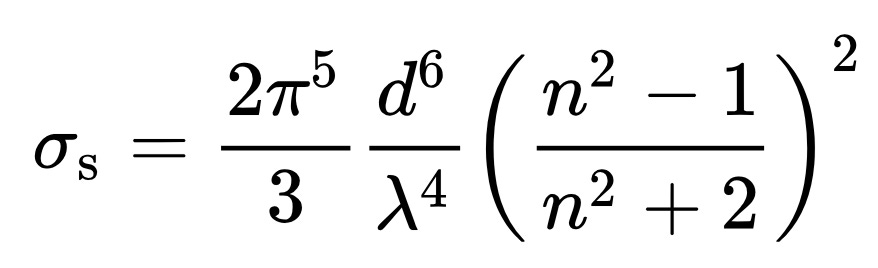The Devil and the Cerulean Sweater

The Devil Wears Prada, Anne Hathaway's cerulean sweater, Rayleigh scattering, and and extraterrestrial solar spectra. Who is right, Dylan or Meryl Streep?

Can Meryl Streep See Color?

The Devil Wears Prada is a 2003 novel and 2006 movie, featuring a young journalist Andrea “Andy” Sachs (played by Anne Hathaway) who lands a job as an assistant to the domineering/borderline abusive fashion magazine executive Miranda Priestly (played by Meryl Streep). The movie follows the personal struggles of Anne Hathaway at her new job as she struggles to decide whether to

1. be a normal person with friends, a significant other, and a work-life balance, or

2. sacrifice her personal life for her job, and follow in the footsteps of Meryl Streep (Satan).

The Devil does not approve of work-life balance.

There’s one scene in particular I’d like to talk about. In this scene, a newly employed Anne Hathaway is taking notes on a meeting involving Meryl Streep and two near-identical greenish belts.

Lucifer, and the greenish belts in question.

The lady in the black coat says something to the effect of “It’s a tough call [choosing between these belts]. They’re so different!” Anne Hathaway, the audience stand-in, snickers, because the belts are damn-near identical, but The Father of Lies Meryl Streep hears her and delivers a blistering reply involving the blue sweater that Anne Hathaway is wearing. I’ll quote the scene in its entirety, to give you a flavor:

Miranda Priestly (examining a dress): Where are the belts for this dress? Why is no one ready?

Jocelyn (holding green belts): Here. It’s a tough call. They’re so different.

Andy Sachs: (snickers under her breath)

Miranda Priestly (turning to Andy): Something funny?

Andy Sachs: No. No, no, nothing’s… you know, it’s just that… both those belts look exactly the same to me. Y’know, I’m still learning about this stuff, and uh… (giggles uncomfortably)

Miranda Priestly: This… “stuff”? Oh, okay. I see, you think this has nothing to do with you.

You… go to your closet, and you select… I don’t know, that lumpy blue sweater for instance, because you’re trying to tell the world that you take yourself too seriously to care about what you put on your back, but what you don’t know is that that sweater is not just blue, it’s not turquoise, it’s not lapis, it’s actually cerulean.

You’re also blithely unaware of the fact that, in 2002, Oscar de la Renta did a collection of cerulean gowns, and then I think it was Yves Saint Laurent, wasn’t it?… who showed cerulean military jackets. I think we need a jacket here.

Nigel: Hmm.

Miranda Priestly: And then cerulean quickly showed up in the collections of eight different designers. Then it filtered down through the department stores, and then trickled on down into some tragic casual corner where you, no doubt, fished it out of some clearance bin.

However, that blue represents millions of dollars and countless jobs, and it’s sort of comical how you think that you’ve made a choice that exempts you from the fashion industry, when in fact, you’re wearing a sweater that was selected for you by the people in this room… from a pile of “stuff.”

It’s a great, character-establishing scene, and it feels relevant, like it’s saying something important. There’s only one problem. Here’s the sweater Anne Hathaway is wearing:

That’s not cerulean! That’s like, royal blue or something! And I can prove it, with physics!

What is Cerulean, anyway?

The word cerulean comes to us from the Latin word for sky, caelum. The color of the sky, caerulus in Latin, entered English as “cerulean.” Thus, the color cerulean should be the color of the sky. But what is the color of the sky?

Blue, right? When you look up at a clear sky, you see some shade of blue color. Why? The answer was discovered in the late 1800s by The Right Honourable Lord Rayleigh, who, besides having a magnificent mustache, was the first to work out the phenomenon of Rayleigh scattering, the scattering of light by particles much smaller than the wavelength of that light.

Lord Rayleigh’s mustache is only a Rayleigh scatterer for terahertz waves and above.

Unpolarized light of intensity I_0 of wavelength λ incident on a spherical particle of diameter d and refractive index n will produce a scattered intensity of

to an observer located a distance R and polar angle θ away from the scattering center.

Note the 1/λ^4 wavelength dependence. This wavelength dependence is characteristic of dipole scattering, the first and simplest type of scattering you learn about in physics. We can summarize this as shorter wavelengths are scattered more. Looking at the visible spectrum, we see that shorter wavelengths are more blue.

If you’re looking at the sky, with the sun at your back, the light that makes it to your eye is dominantly light scattered by the atmosphere, of which blue light scatters more than red light. Thus, the sky you observe is blue.

Deriving the Color of the Sky

Going a little further, we can use the expression for Rayleigh scattering to derive the color of the sky on a sunny day.

Since molecules in the atmosphere are randomly oriented, one may integrate the Rayleigh scattered intensity over a bounding sphere enclosing the molecule, and derive an average scattering cross section, an effective cross-sectional area for collision frequency/scattering amplitude.

Now, if we’re discussing Rayleigh scattering in the atmosphere, it is convenient to express this scattering cross section in terms of α, the molecular polarizability, which is a nice property for estimating scattering of elemental gases.

in cgs units

The fraction of scattered light per unit length, as a function of wavelength and polarizability, is then

where N is the number of particles per unit volume.

Earth’s atmosphere is roughly 78% nitrogen (N2), 21% oxygen (O2), and 1% argon (Ar), and so if you know the molecular polarizability of each gas, you should be able to derive the spectrum of scattered light seen by your eye. That’s what we’re going to do — we’re going to calculate cerulean from first principles, and prove that Meryl Streep is wrong about the color of Anne Hathaway’s sweater.

The Plan of Attack

To calculate the color of blue sky, which I will call true cerulean, we’re going to follow this plan.

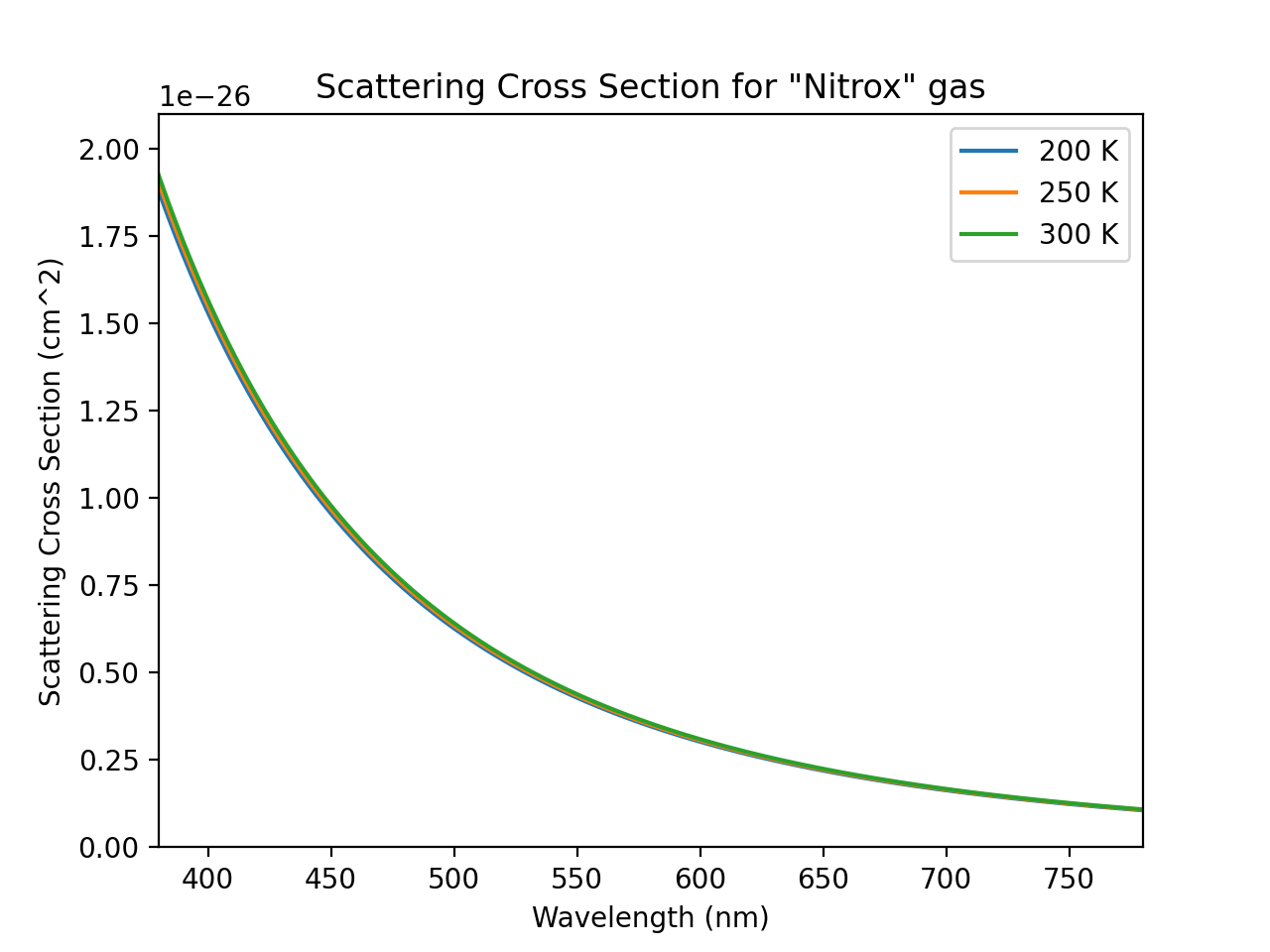
1. The atmosphere is mostly nitrogen and oxygen, so we calculate an effective scattering cross section for both nitrogen and oxygen gas.

2. Since the atmosphere is ~79% nitrogen and ~21% oxygen (let’s just ignore Argon), we can take a weighted average of these two scattering cross sections to get an average scattering cross section for “Nitrox” gas, which will be our proxy for atmospheric scattering.

   1. The scattering coefficient per unit length is linear in the scattering cross section, so the cross section vs. wavelength will tell us the relative fraction of scattered power vs. wavelength with no further math needed.

3. We then multiply this scattering function by the sun’s emission spectrum, producing the spectrum of solar light that is Rayleigh scattered into our eye. We’re going to ignore absorption and multiple scattering events.

   1. We’re also going to model scattering from water vapor, properly Mie scattering, as wavelength-independent scattering, which I’ll incorporate into the scattered spectrum.

4. Finally, we take this calculated scattered light spectrum, and use a Python package to convert this spectrum into an RGB color that we can display on our computer screen, and compare to Anne Hathaway’s sweater, thus proving Meryl Streep wrong.

Calculating Scattering Cross Section

First, we estimate the scattering cross sections of N2 and O2, the dominant atmospheric gases. Since the atmosphere varies quite a bit in temperature from the ground to low-earth orbit, I first looked at the temperature dependent molecular polarizability coefficients. I found this paper¹, in which there is a nice table giving us the molecular polarizability volume for various gases from about 200 Kelvin to 360 Kelvin, perfect for atmospheric temperatures.

Table 1: Values of molecular polarizability volume vs. temperature for ~200K to ~360K from Hohm et. al.

A NASA technical note from 1977² provides a helpful table of measured absolute scattering cross sections for various atmospheric gases against which we can check any estimations we make using these values.

Table 2: Ground truth values of Rayleigh scattering cross section from a 1977 NASA technical note

Here’s a plot of the scattering cross sections estimated at 300 Kelvin (room temperature) for nitrogen and oxygen gases, with the 1977 NASA data as reference points.

Rayleigh scattering cross sections, using the expressions in Table 1 for molecular polarizability volume, evaluated at 300K.

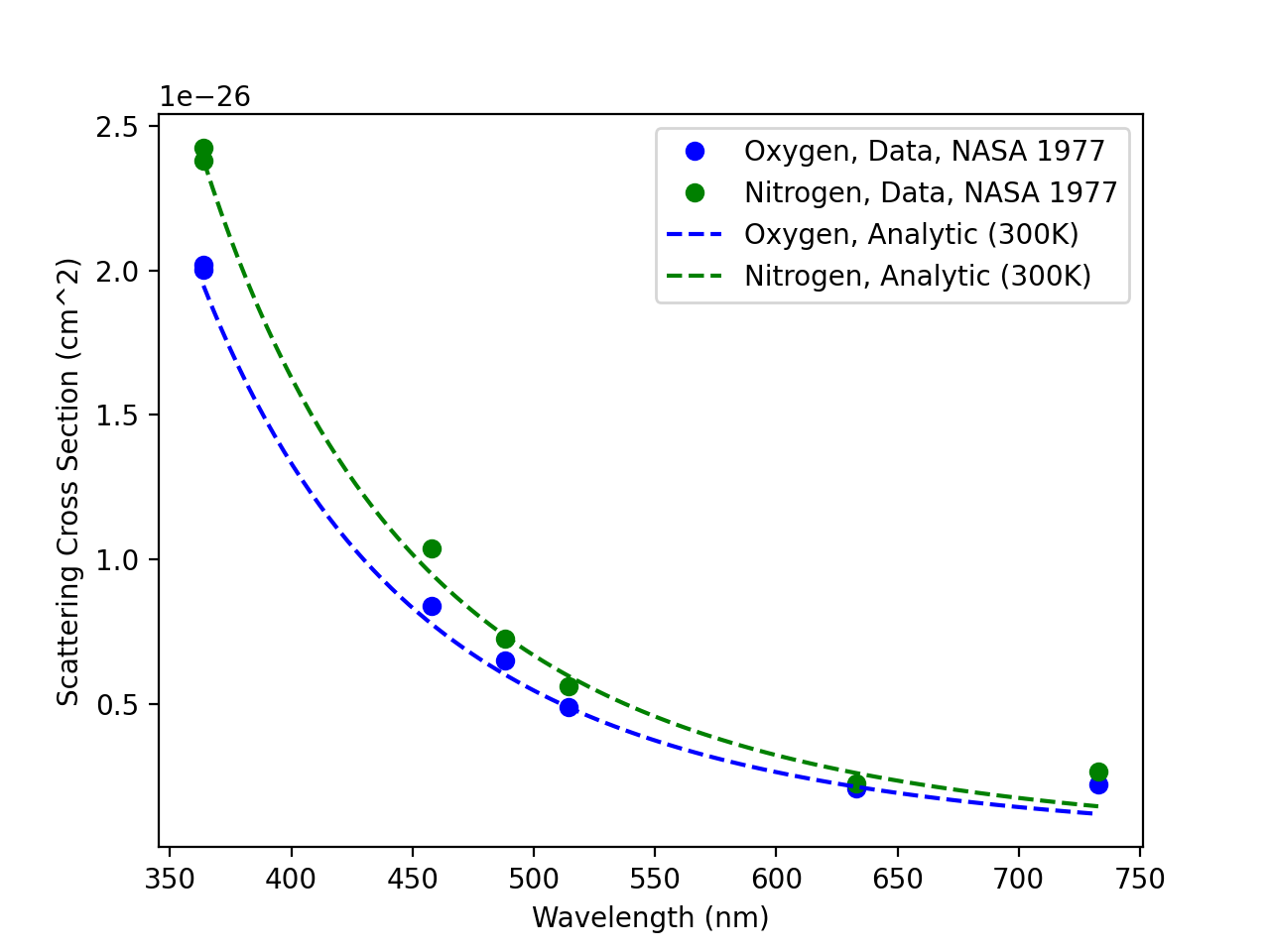
Looks good! Let’s average these two gases into our “Nitrox” effective scattering cross section, and check its temperature dependence to make sure it’s not a problem.

It looks like the effects of temperature are pretty much negligible. Great, let’s ignore it.

Solar Spectrum

Now, in order to calculate the spectrum of light that reaches our eye, we need the spectrum of the sun. I’m going to use the data from the National Renewable Energy Laboratory (NREL)’s page on solar spectra. They actually give us three measured spectra, the “Extraterrestrial,” the “Global Tilt,” and the “Direct + Circumsolar” spectra.

Solar irradiance from NREL’s page on Reference Air Mass 1.5 Spectra

I had no idea what the difference was between these three, so I asked ChatGPT.

1. Extraterrestrial: This is the solar energy that is incident on the Earth's atmosphere outside of the atmosphere, assuming no atmospheric absorption or scattering. It is essentially the solar spectrum that would be observed if you were in outer space and measuring the sunlight before it interacts with the Earth's atmosphere.

2. Global Tilt: Global Tilt represents the spectral irradiance of solar energy that is received on a surface tilted at a specific angle (in this case, 37 degrees) towards the sun, taking into account the atmospheric conditions specified in the data. This is essentially the solar energy spectrum incident on a surface that is oriented to capture sunlight for energy generation. It includes both direct sunlight and diffuse (scattered) sunlight, which is why it's referred to as "global."

3. Direct + Circumsolar: Direct + Circumsolar represents the spectral irradiance of direct solar radiation along with the circumsolar component. Direct solar radiation is the sunlight that arrives directly from the sun without scattering. The circumsolar component includes the direct solar radiation and the portion of scattered sunlight that is within a certain angular range around the sun. This component is particularly relevant for concentrating solar technologies that track the sun's position in the sky.

We’re going to choose the Extraterrestrial spectrum, because that seems like the cleanest, unscattered one. But just for completeness, I tried this whole analysis with each of the different spectra and it made no difference to the final color.

Rayleigh and “White” Scattered Spectra

We’re basically done, all that remains is to multiply our scattering cross section with the solar spectrum, and find out what color that is. I’m going to normalize everything because only the relative scattered power in each wavelength matters.

Additionally, I’m now going to try to take into account water vapor scattering. Water droplets in the atmosphere are much larger than a single molecule (think clouds), and are basically “white” scatterers, meaning they scatter all wavelengths roughly equally (Clouds, for example, are white). Thus, we can estimate the scattered light from a cloud or background haze as just some fraction of the solar spectrum, which is much easier than going through the whole formalism of Mie scattering.

We’ll calculate the scattered spectrum, then feed it into some python code that converts it to a color!

Scattered intensity for Rayleigh scattering and for “white” scattering.

You’ll notice I plotted three spectra here. The blue spectrum is precisely what I said earlier, the product of our Rayleigh scattering cross section with the Extraterrestrial solar spectrum, truncated to the 380 nm — 780 nm range, the limit of what a human eye can detect.

However, to be compatible with the color-estimation code, I had to construct a 5 nm moving average, and that’s what the two “averaged” spectra are. The orange and green spectra, respectively, are the Rayleigh and “white” scattered intensities.

From Spectrum to Color

Now as you may know, most displays use an RGB system for displaying color. If you’ve never looked at your computer screen really closely, try putting a small drop of water on your computer screen. It will act as a magnifying glass and allow you to see the little red, green, and blue pixels that make up your display.

Water droplets on a computer screen, showing the RGB pixels.

Following this Python tutorial from scipython.com³ I’m going to use something called the CIE 1931 Color Matching Functions to map spectral power onto red, green, and blue RGB pixel intensities.

Now the RGB method of color display is pretty good, but it isn’t perfect. The set of colors which the RGB system can display is smaller than the full set of colors the human eye can see.

The CIE chromaticity diagram below explains the system. The irregular blob is the colors visible to the human eye, and the triangle is the “gamut” of colors permissible in an RGB system. The vertices of the triangle represent the “pure” pixel colors.

In any case, using the color matching functions, we can come up with the actual color of our calculated spectrum and compare it to Anne Hathaway’s sweater. Take that, Meryl.

So, is the Sweater Cerulean?

And now, the moment of truth.

Uh, hmm, you know, the true cerulean I calculate is really quite close to Anne’s sweater color there. Shit, I think Meryl Streep might have been right.

Okay, wait, we can do a little better. Earlier, I explained that water droplets in the atmosphere are pretty close to “white” scatterers (wavelength-independent), and they make up some proportion of the scattered light in your eye. We can average the Rayleigh scattering spectrum with the white scattering spectrum, and come up with a range of colors that can be considered cerulean.

You know, they’re all really close to that sweater color under different lighting, except the last few. The fully “white” scattering kinda looks like Los Angeles on a bad day, or light near the horizon.

A picture I took overlooking the Missouri river from New Orleans. You can definitely see a transition, and it does kinda look like the Rayleigh→Mie scattering transition I plot above.

Well, uh, it’s a good thing I’m not Meryl Streep’s assistant, because I would have wasted like 8 hours of work time trying to figure out what color cerulean is, only to find out it’s exactly what she told me.

There’s probably a life lesson in there somewhere, but I’m not sure what it could be.

1. Hohm, U., & Kerl, K. (1986). Temperature dependence of mean molecular polarizability of gas molecules. Molecular Physics, 58(3), 541–550. doi:10.1080/00268978600101351

2. Shardanand and A. D. Prasad Rao. Absolute Rayleigh scattering cross sections of gases and freons of stratospheric interest in the visible and ultraviolet regions. March 1, 1977, Document ID 19770012747

3. https://scipython.com/blog/converting-a-spectrum-to-a-colour/