The Tyranny of the Wagon Equation: Pre-Gunpowder Military Logistics and the Minimum Donkey Rate
A mathematical extension to ACOUP's recent blog post on military logistics
The Problem
While reading Bret Devereaux’s excellent blog, A Collection of Unmitigated Pedantry (ACOUP), I came across this article on pre-gunpowder army logistics. This article is concerned with the physics of feeding a large mass of hungry human beings (an army) at some large distance from a food source (a base). Basically, food transport logistics before railroads.
Here is the central problem in army logistics, as stated by Devereaux:
The problem in a nutshell is that anything available to these armies prior to the advent of the railroad that can carry food, also eats food... We may call this problem the ‘tyranny of the wagon equation.’
“The tyranny of the wagon equation” purposefully invokes a truism concerning the difficulty of supplying rockets with fuel, the “tyranny of the rocket equation.”
What is this tyranny? Why is rocketry so demanding?
The Tyranny of the Rocket Equation
The classical (non-relativistic) rocket equation concerns the mass ratio of fuel to payload necessary to increase a rocket’s speed by some “delta-v.” Let’s derive it, and experience tyranny.
A chemical rocket works by expelling “exhaust” (mass) at some speed v_exhaust relative to the rocket to increase the speed of the remaining rocket mass. Here’s a diagram in the reference frame of the rocket.
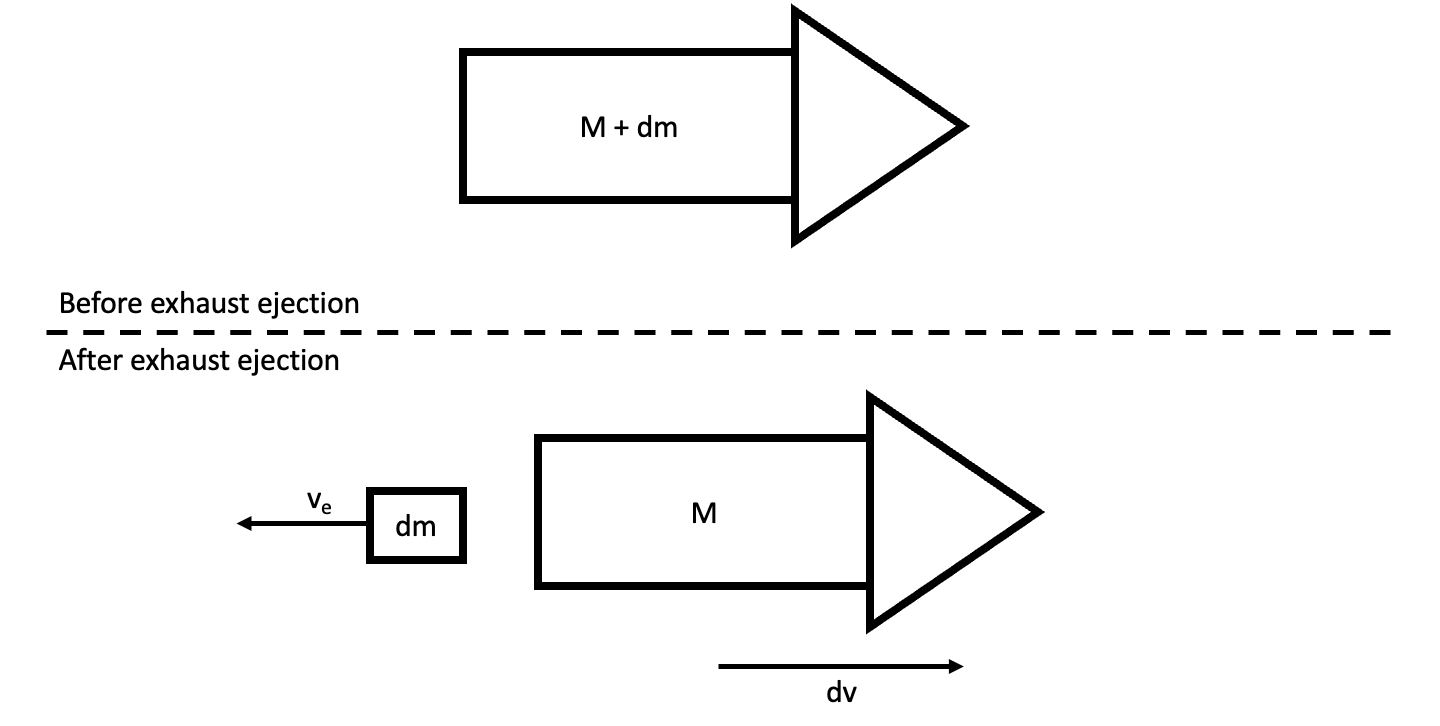
Conservation of momentum requires the following equation to be satisfied:
We can separate the variables in this expression:
And set up an integral, where the rocket gains speed delta-v, and the rocket mass goes from initial mass M0 to final mass Mf:
However, the dm written above is the differential mass of the exhaust, not the rocket. We must always integrate over like quantities, and as the exhaust gains mass, the rocket must lose mass:
This equation integrates to the classical rocket equation:
M0 is the initial mass of the rocket, which we will define as the mass of the fuel plus the mass of the payload:
The final mass is simply the mass of the payload. This allows us to rewrite the rocket equation as:
This is the tyranny of the rocket equation. As the amount of delta-v (change in rocket speed) increases, exponentially more fuel-to-payload ratio is required.
The Tyranny of the Wagon Equation
Pre-modern military logistics is surprisingly similar to non-relativistic rocketry.
A man in the army, for example, a Roman soldier, cannot carry three months worth of food — he must be supplied by some home base. If he carries a maximum of ten days of food, and walks at a speed of 20 miles per day, his effective range limit is 200 miles, hard stop. Supply trains are therefore necessary, and donkeys are much better at carrying food than humans are.
However, donkeys also eat food. So how much do they extend the effective range of an army? This point is discussed in Devereaux’s blog post (so please read it for details), but the essence is found in this quote concerning wagons drawn by animals:
Assuming two-horse 1400 lb wagons… for a group of thirty infantryman the [addition of] the first wagon [to the supply train] doubles their range from 120 to 240 miles… Doubling again to around 400 (accounting for horse rest time) requires not two but six wagons for thirty men. To double the range again would require more wagons than men.
We have some sort of exponential growth here, just like the classical rocket equation. Unfortunately, the original post does not proceed to derive the classical wagon equation and discuss its scaling laws. Fortunately, I will.
Derivation of the Classical Donkey Equation
Single Donkey Physics
Let’s consider a single donkey who eats food at a rate δ.
If he can carry at most a quantity of food f0, then the food carried by the donkey as a function of time is:
If the donkey moves at a speed v, then the food carried by the donkey to some distance L is:
Imagine that you want to deliver a food parcel of size Δf. Assume that the donkey only consumes food until his parcel of food is delivered at some distance L from his home, and then the donkey vanishes. This assumption is unphysical, because the donkey also has a return journey, but the food consumption rate δ can simply be doubled later to account for this.
The distance L at which the donkey can deliver Δf food is then:
Let’s define some terms.
For a single donkey, this is simply the absolute maximum distance at which the food can be delivered.
Two Donkeys are Better than One — Pairwise Donkey Transfer
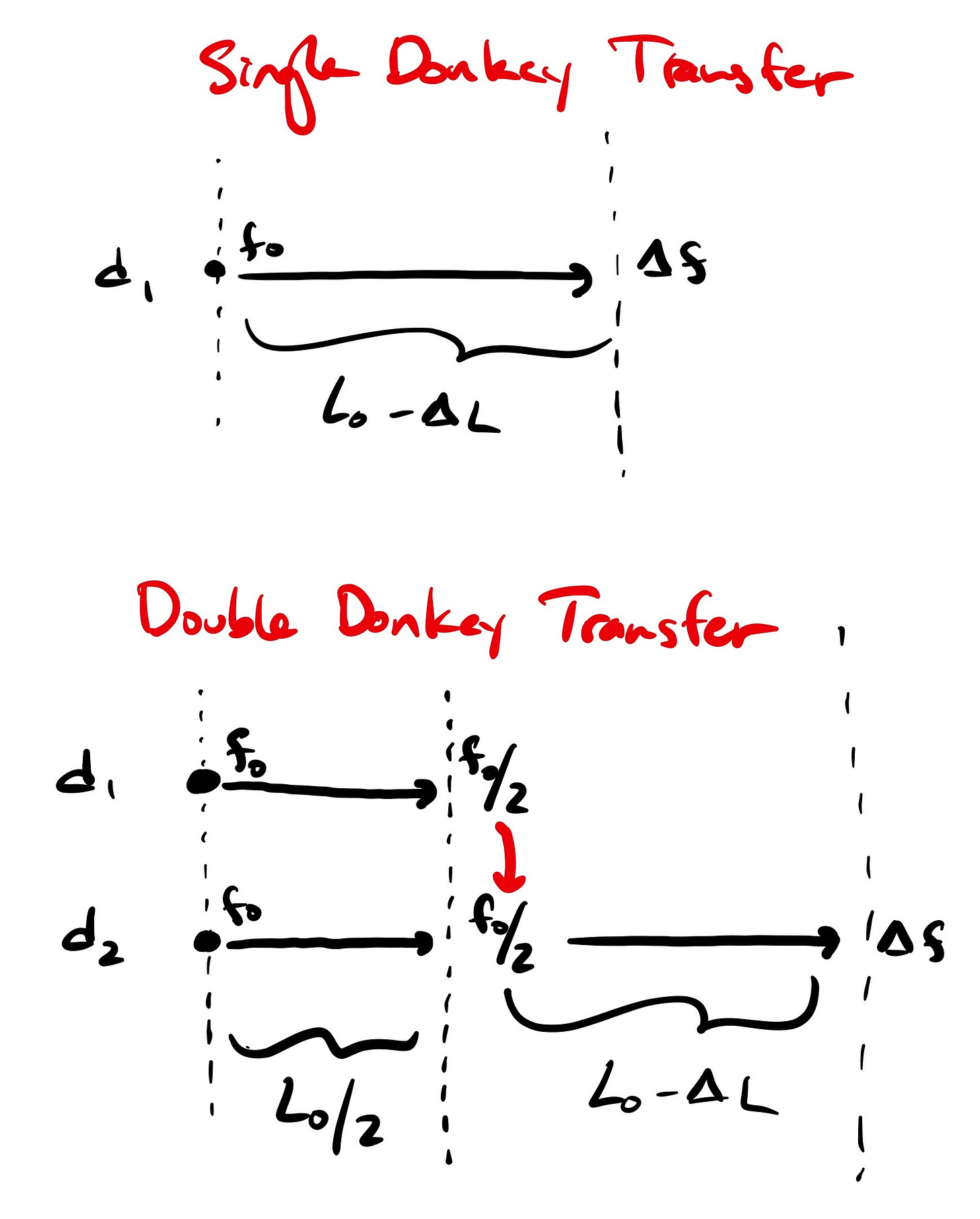
Two independent donkeys can clearly deliver 2Δf food the same distance L from their home base. However, by transferring food between donkeys, the maximum range of a single food parcel can be extended.
A single donkey begins with f0 food, travels a distance L0 - ΔL, and delivers his food parcel of size Δf.
However, in the two-donkey method, both donkeys initially with f0 food travel a distance L0/2, at which point each donkey has f0/2 food remaining. At this point, donkey 1 transfers his food to donkey 2, who now has f0 food, and donkey 2 travels an additional distance L0 - ΔL, for a total distance of 3/2 L0 - ΔL.
In the quadruple donkey transfer, this transfer step is repeated twice. Four donkeys set out and travel L0/2. Two donkeys transfer their food to the other two, who travel an additional L0/2. One donkey then transfers his food to the remaining donkey, who travels the remaining L0 - ΔL, for a total distance of 2 L0 - ΔL.
The pattern should be obvious. Each doubling of donkeys (exponential growth) adds an additional L0/2 distance (linear) at which the food parcel Δf can be delivered.
Note: This method of donkey transfer (the pairwise method) is NOT optimal! See the section on Harmonic Donkey Transfer for an even better algorithm.
Let the number of initial donkeys D0 be described as
for some integer k. The distance traveled by the final donkey/food parcel is then given by
for the same integer k. Eliminating k, we find the maximum distance traveled by a food parcel as a function of initial donkeys
We can rearrange this expression, and reinsert the definitions of L0 and ΔL to find the number of initial donkeys D0 for a given supply distance L to be:
The tyranny of the donkey equation is now obvious — it requires exponentially more donkeys to move a food parcel linearly further.
Supplying the Army
Now let us consider an army made up of N men at a distance L from the supply base, all of whom eat food at a rate α. The total food consumption rate is then Nα, which must be matched by the food current flowing into the army camp. The food current (influx of food into the camp), is equal to the size of the food parcel Δf times the donkey influx rate d (in donkeys per unit time) at the supply chain endpoint.
We know that each endpoint donkey corresponds to some number of initial donkeys, and so donkeys per unit time must follow the same ratio:
Thus we can write an expression for the necessary rate of donkey flow d0 out of home base to supply an army at a distance L.
The Minimum Donkey Rate
The donkey rate can be minimized over the food parcel size Δf. Taking the derivative of d0 with respect to Δf and setting it equal to zero yields a simple expression,
or, in numerical form, Δf/f0 ~ 0.72 .
Plugging in this optimal food parcel size gives us, finally, the minimal donkey rate, or the rate at which donkeys must be emitted from the source base to supply an army at a distance L from the base:
This equation can be plotted in non-dimensionalized form (first setting f0 to 1) to examine the exponential growth of the required donkey rate d0.

An exponentially increasing donkey rate is required for long supply lines, or slow and hungry donkeys.
As your donkeys get hungrier (delta), slower (v), or have to travel farther (L), exponentially more donkeys are required to supply your army. A civilization which can supply a normalized donkey rate of 100, sufficient for a normalized donkey supply distance of 4, is vanishingly unlikely to be able to handle a donkey rate of 100,000, for a mere doubling of the normalized donkey supply distance.
Harmonic Donkey Transfer
Our strategy of shifting the food burden among donkeys was pretty good, but an even better algorithm exists, that uses the harmonic series.

The first two cases of harmonic donkey transfer (HDT), with one and two donkeys, is identical to the pairwise donkey transfer algorithm.
Now consider the case of three donkeys. If the donkeys all walk a distance L0/3, then each donkey has 2/3 f0 food remaining. Donkey 1 can then transfer his food (equally) to donkeys 2 and 3, who then each travel L0/2, the transfer occurs again between donkeys 2 and 3, and finally the last donkey (3) travels L0 - ΔL to deliver the food parcel.
For the harmonic donkey transfer case, the maximum travel distance is instead given by the following series:
For the four-donkey case, this comes out to 25/12 L0 - ΔL. Note the presence of the summation of 1/n as n goes to number of donkeys D0. This series is called the harmonic series, hence the name “harmonic” donkey transfer.
The original “pairwise” donkey transfer algorithm yields a maximum travel distance of:
For the case of four donkeys with pairwise transfer, we find L = 2 L0 - ΔL.
Thus, the harmonic donkey transfer, using four donkeys, yields a maximum transport distance 1/12 * L0 longer than the pairwise donkey transfer.
We can go further — in the limit of large numbers of donkeys, we can use a partial sum formula to estimate the travel distance as a function of donkey number directly. Specifically:
Here, γ is the Euler–Mascheroni constant, roughly equal to 0.577. Thus, our maximum donkey travel distance for the harmonic donkey transfer can be written as:
This equation can then be substituted into the expression for feeding the army in the same manner as the pairwise donkey transfer algorithm, but requires the use of special functions for inverting this transcendental equation, and the expression is rather nasty.
Here’s what I got for the necessary donkey rate out of home base for an optimized HDT donkey load size:
Let’s also plot the minimum donkey rate on a semi-log plot:
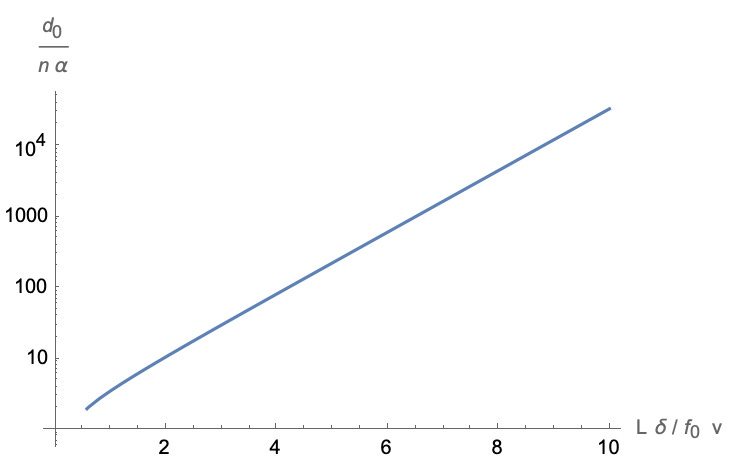
This is much better! Many fewer donkeys are required to supply our army with harmonic donkey transfer.
Comparing Harmonic Transfer to Pairwise Transfer
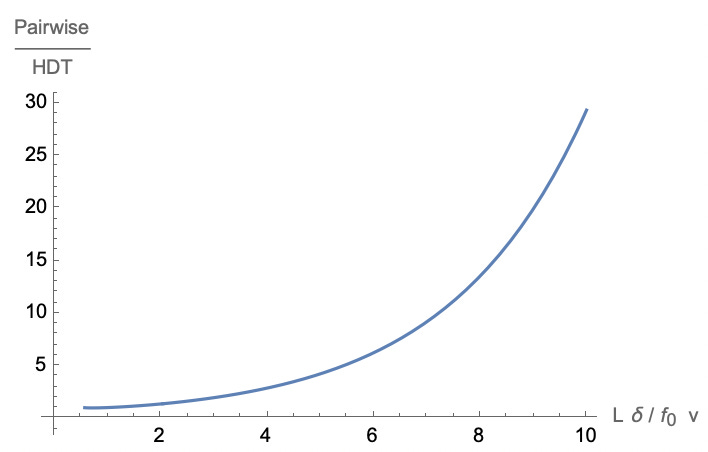
How much better is the HDT strategy than pairwise transfer? We can plot the ratio of the minimal donkey rate d0 for pairwise transfer to HDT, i.e.
Wow! The harmonic donkey strategy is much better than the pairwise donkey strategy for large distances, hungry donkeys, or slow and weak donkeys! For a normalized distance of 8, 15 times fewer donkeys are required to supply the army. This super-linear improvement of harmonic donkey transfer over pairwise transfer actually makes me doubt my math a little, because it’s so much better. If any donkey mathematicians would like to check me on this one, let me know!
The Relativistic Donkey Equation
Now, all of the preceding discussion assumes classical donkeys moving at a very small fraction of the speed of light. How does the physics change when the donkeys become relativistic?
I’ll save that one for a later post.












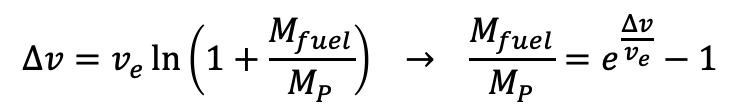




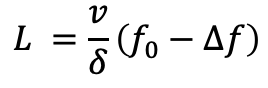
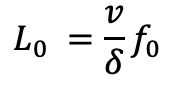
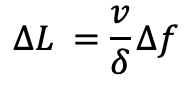
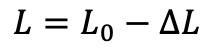


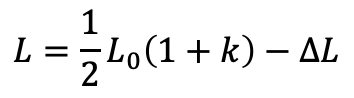



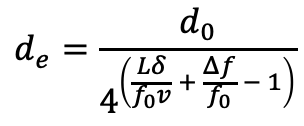



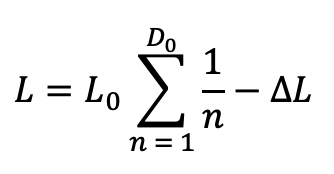






I believe the Breguet aircraft cruise-range equation is another important example of this, and why it is crucial that in-flight refueling, or re-charging, or co-thrusting by supply module craft, be introduced. We waste colossal (exponential) amounts of fuel by trying to carry it all with the aircraft. The technology for safe reliable automatic in-flight refueling or recharging his well proven for both manned operation (NASA Dryden, USAF) and UAVs to manned( eg DARPA).
It would be a telling calculation to estimate how much Geoff fuel and pollution could be saved if aircraft just carried or reasonable amount of fuel and refueled in-flight, saving both of fuel they were carrying in the airframe weight and complexity that that required which then meant smaller jet engines which means less weight which means less fuel which means less airframe…
It seems unlikely that classical and medieval generals (or anyone at that time) had the mathematical knowledge to optimize this with the harmonic, though it's possible that it could have been worked out by combining many different generals' trial and error.