Dungeons & Dragons, Peasant Accelerators, and Inertial Confinement Fusion
Mixing Real-World and D&D Physics for Fun, Profit, and Nuclear Power Sources
Dungeons and Dragons, along with other tabletop roleplaying games, has a very particular failure mode known as “the Munchkin.” A Munchkin is someone who bends the game rules to the breaking point, someone who is trying to “win” D&D. When you are the Dungeon Master, this can be very annoying.
That being said, I love bending the rules of D&D.
Let’s say you’re an adventuring party about to fight the Final Boss of your campaign. He’s holed up in an impenetrable Fortress of Doom, with walls too strong to breach and too high to climb. What kinds of superweapons do the physics of D&D allow us to build?
The Peasant Railgun
First off, we have the “Peasant Railgun.” It’s a technically legal idea in D&D that allows you to fire rocks at high velocity using only the power of peasants.
In D&D (Fifth Edition, or 5e for short), time is divided up into “rounds,” lasting precisely 6 seconds. Each character has a set number of “actions” that can be performed in that 6-second round. The actions occur sequentially, not simultaneously.
Consider n peasants standing in a row, spaced five feet apart. Peasant 1 holds a rock. At the start of the round, Peasant 1 takes his action, and hands his rock to Peasant 2. Peasant 2 then takes his action, handing the rock to Peasant 3, and so on and so on until Peasant n.
Due to the unique way the D&D 5e rules work, all of this rock-passing occurs in one 6-second round. Thus, if the rock travels n * 5 feet in 6 seconds, the rock must be traveling at a velocity of n * 0.254 m/s.
The peasant railgun holds that if you have enough peasants, you could conceivably fire a rock at near-lightspeed and obliterate whatever you point the peasants at.
Unfortunately, this peasant weapon is fairly unimpressive. Let’s do the math.
Classical Peasant Accelerator
The rock moves 5 feet for each peasant in the railgun over the course of 6 seconds. So, we have the velocity of the rock after the nth peasant as
So how fast can we get the rock going? An average medieval village probably had 50-100 people, so if you’re out adventuring, you have to round up some peasants, and let’s put the maximum amount that you can easily find at n = 100. Calculating this out, the 100-peasant railgun fires the rock at about 25.4 m/s.
Let’s say the rock weighs about 1 pound. Using the formula for classical kinetic energy:
This gives us a kinetic energy of about 150 Joules.
This is a pretty pitiful amount of energy. For context, a major-league baseball pitch travels closer to 40 m/s, and a baseball is about a third of a pound, so a baseball pitch has about double the energy of our peasant railgun.
American Civil War Cannon Equivalent
How many peasants would it take to do something impressive? In the American Civil War, a standard 12-pounder Napoleon gun could fire a 12 pound projectile at 453 m/s. This is about 560 kJ of energy per projectile.
Let’s say we tried to fire the same 12-pound projectile with our peasant railgun — we would need 1,783 peasants standing in a 2.7 kilometer-long line to equal the muzzle velocity of the cannon.
Tunguska Airburst Equivalent
How about an extreme case where I need to destroy a city/evil fortress — how many peasants do we need to create a Tunguska event? For those who don’t know, the Tunguska event was a 12-megaton explosion that occurred in Russia in 1908, generally attributed to a meteor airburst. It is the largest impact in recorded history, and it has some freaky pictures associated with it.
The Tunguska Event was a 12 megatons-of-TNT explosion, or 5 * 10^16 Joules. This would obliterate a major metropolitan area, and also probably the Fortress of Doom inhabited by the Final Boss.
For the classical peasant railgun, could we create a Tunguska-level projectile? Using the above equations for kinetic energy:
If the peasants are once again firing a 12-pound cannonball, it needs to be fired at ~1.35 * 10^8 m/s, or about 40% the speed of light. Oh, and you’d need about 550 million peasants in a 500,000 mile-long line to do it.
So… technically yes?
Relativistic Peasant Railgun
Sadly, the classical peasant railgun is not a particularly good option, as far as physically plausible theories go.
Here’s the expressions for the classical peasant accelerator.
These expressions have a two problems:
they break down when our projectile reaches a significant fraction of c
they assume fixed velocity gain per peasant
We can actually solve both problems simultaneously, but first, let’s calculate the change in energy at each peasant in line to see the problem.
If we calculate the change in kinetic energy for the nth peasant, we find that it scales linearly with n, meaning that each successive peasant must do linearly more work that the previous peasant to keep the same velocity gain. This isn’t very physical (peasants can’t do infinite work per the D&D 5e rules), and it’s not how real-world accelerators are designed either.
Instead, let’s postulate that each peasant adds a fixed amount of energy to the rock. Let’s choose this energy kick to be 1/2 * m * v_0^2, where m is our 12-pound cannonball and v_0 is 0.254 m/s. This is equal to about 175 mJ.
In relativistic mechanics, the energy of an object is no longer described by the classical 1/2 m v^2, but by Einstein’s formula.
The energy of an object moving with speed v is given by the relativistic mass-energy equivalence, which is usually quoted as just E = m * c^2. In reality, this is the energy of an object at rest. When an object is in motion, its energy is given by E = m * c^2 * γ, where γ is the Lorentz factor, a dimensionless parameter which describes time dilation, length contraction, and all the other weird relativistic effects.
So here is our peasant energy gain and total projectile energy:
Substituting in Einstein’s formula, we find:
And solving for velocity, we find:
Now our peasant railgun scales correctly at the higher speeds — we can see that the velocity of the rock approaches, but never quite reaches, the speed of light.
With this modified formalism, a Tunguska-level peasant railgun requires 3*10^17 peasants arranged in a 46 lightyear-long line. Very, very impractical, and the Final Boss in his Fortress of Doom feels very secure.
Apropos of nothing this TikTok is actually a really good visualization of how a circular particle accelerator works.

Magical Nuclear Fusion
All right, so the peasant railgun is fairly unimpressive in my view for wholesale destruction. You need a 50 lightyear long line of peasants just to destroy a city.
Instead, what if we tried to make a star?
Enlarge/Reduce
There’s a spell in D&D 5e called Enlarge/Reduce. Here’s the text from roll20.net.
The important bit is in the third paragraph:
The target’s size doubles in all dimensions, and its weight is multiplied by eight… If there isn’t enough room for the target to double its size, the creature or object attains the maximum possible size in the space available.
Now let’s note a couple things. First, the object’s weight octuples, indicating that there is eight times more mass of whatever the thing is. Second, the object attains the maximum possible size in the space available.
Next, let’s look at the Wall of Force spell.
This spell can be used to make a bubble which is impenetrable and immune to all damage.
With a sufficiently permissive reading of the D&D Fifth Edition rules, I claim this can be used to make a sun.
Inertial Confinement Fusion
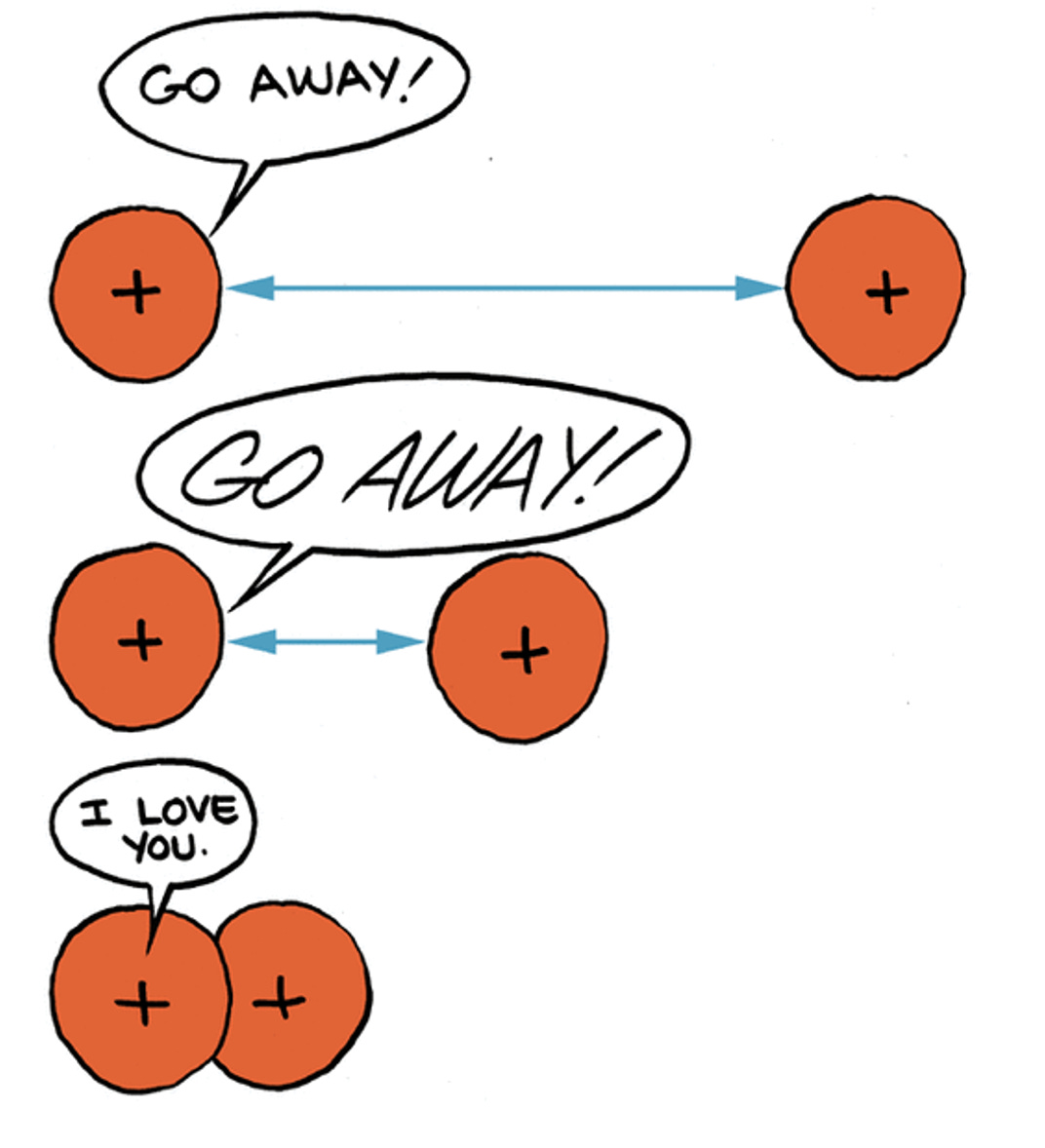
The basic premise of Inertial Confinement Fusion (ICF) is surprisingly well summarized by this silly cartoon.
Basically, if you take two nuclei, usually Deuterium and Tritium in modern experiments, and shove them together with enough force to overcome the Coulomb Barrier, they’ll fuse into one new nucleus, a free neutron, and some excess energy.
What is the Coulomb Barrier? It’s the energy required to overcome the electromagnetic repulsion of the nuclei, and force the atomic nuclei into contact.
Rock Fusion and Binding Energy
So let’s say I want to make a fusion reactor using rocks as fuel. For the sake of argument, I’m going to say that rocks are mostly SiO2, silicon and oxygen.
Certain stars already use silicon in fusion reactions, in what’s called a “silicon burning” reaction. From Wikipedia:
silicon burning is a very brief sequence of nuclear fusion reactions that occur in massive stars with a minimum of about 8–11 solar masses…
Silicon burning begins when gravitational contraction raises the star's core temperature to 2.7–3.5 billion kelvin (GK). The exact temperature depends on mass. When a star has completed the silicon-burning phase, no further fusion is possible. The star catastrophically collapses and may explode in what is known as a Type II supernova.
Cool! So if I want to make a D&D sun, I need to raise the temperature of some rocks to 3 billion degrees Kelvin. It will then form a brief miniature sun, collapse in on itself, and (maybe) go supernova. No problem!
A Side Note on the Energetic Favorability of Fusion vs. Fission
Silicon burning is the last stage of stellar fusion because fusion becomes energetically unfavorable after this step. This chart explains why that is.
The y-axis plots the binding energy per nucleon of all the elements (protons and neutrons are both nucleons).
The binding energy is a trickier concept, and can be understood like this:
A Helium-4 nucleus is composed of two protons and two neutrons.
Using E = mc^2, you can calculate the difference in energy between both sides of this equation.
As you can see, the energy of the two protons + two neutrons is slightly higher than the energy of the helium-4 nucleus — that difference is called the “binding energy.” The binding energy per nucleon of Helium-4 is then 28 MeV / 4 nucleons = 7 MeV / nucleon.
So in a nuclear reaction with reactants and products, as long as you are increasing the binding energy of your products relative to your reactants, your reaction can occur. The slope of the chart basically tells you when it’s favorable to go up in atomic number, or down.
We see that iron is at the peak of the binding energy curve, which means that elements heavier than iron undergo fission and elements lighter than iron, like silicon, undergo fusion.
From the binding energy chart, we can also see that it would be much easier to use water as fuel for our D&D sun, because water is composed of lighter elements with lower binding energy (hydrogen and oxygen), but let’s do it with silicon rocks for fun.
Enlarge, enlarge, enlarge
So what happens if I put a bunch of rocks inside of a Wall of Force, and cast Enlarge on them a few times?
Well, as we read from the spell description, the mass of the rocks will octuple. Since they’re encased in a Wall of Force, their volume must stay the same, and so I claim that their density is also multiplied by 8.
Now, the Rules As Written for the Enlarge/Reduce spell state “if there isn’t enough room for the target to double its size, the creature or object attains the maximum possible size in the space available.”
I interpret this rule to mean that the rocks will grow to fill the Force bubble, and then continue increasing in density and compressing themselves until their mass has increased by a factor of 8.
Now remember we need a ~ 3 billion Kelvin temperature. How can we relate density to temperature, so we can figure out how much density we need?
Ideal Gas Law for Plasmas
Well, anything sufficiently hot is a gas, and so we can apply the Ideal Gas Law.
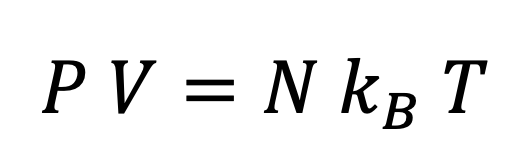
Substituting in a convenient expression for density, we find a modified ideal gas law that reads:
This allows us to relate the temperature, density, and mass of our silicon atoms to their pressure. Why is this helpful? What pressure do we have to overcome to initiate fusion?
The Coulomb Barrier
The “pressure” we need to overcome for fusion is precisely the Coulomb Barrier! Now, the Coulomb Barrier is the electromagnetic force that repels nuclei from each other, and it’s usually expressed as an energy:
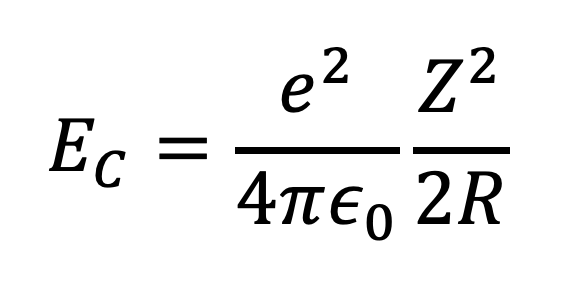
Since we need a pressure, not an energy, and pressure is just energy density, we need to divide this energy by a volume. The only physically relevant volume I can think of is the volume of the nucleus, so I guess we’ll use that for a first-order approximation.
This Coulomb Pressure will be the pressure we need to overcome the Coulomb Barrier and initiate nuclear fusion.
By the way, I’m happy to have someone who knows better than I do check me on this — my field is accelerator physics, not fusion!
Putting it all together
Equating the Coulomb Pressure to the Ideal Gas Law gives us an expression for the required critical density to overcome the Coulomb Barrier and initiate silicon-burning fusion. Here it is:
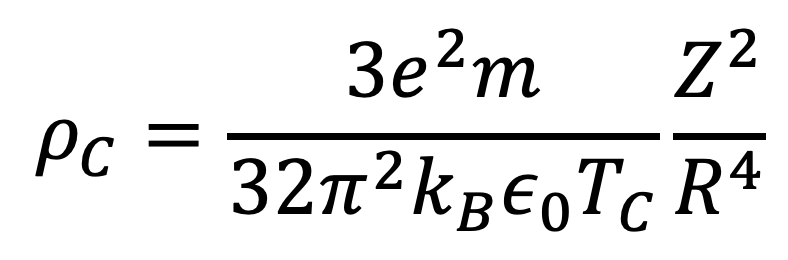
Putting it all together gives a critical density of about 10^17 g/cm^3. Normal rocks have a density of about 2 g/cm^3.
Now since I claim that the density of the rocks increases by a factor of 8 every time we cast Enlarge, then all we need to do is find out how many octuplings of density we need, starting from a rock, to make a star.
As it turns out, the answer is 19.
A Star is Born
Okay, so what does this look like?
I imagine you have a cabal of twenty wizards for this spell. The first wizard picks up a bunch of rocks, or really anything, and places them on the ground. He casts Wall of Force to create a small, impenetrable bubble around the rocks. The other 19 wizards then cast Enlarge on the rocks all at once, and poof! A miniature sun appears! It also develops its own gravitational pull, as the pile of rocks will weight about 10^18 kg. This is about the weight of a small moon.
The silicon-burning process happens incredibly quickly — a massive star will burn all its silicon in less than 1 day, after which it will go supernova. Thus, I expect this pile of rocks, with much less mass, to explode basically immediately, and if the primary caster dispels Wall of Force, it will probably destroy anything near it, up to and including the casters.
How much energy is released? Well, according to my estimates of binding energies, this is something like 80 MeV per silicon atom, and there’s 10^18 kg of silicon there. That’s about 10^32 Joules, or ~2% of the output of the sun in one year.
For some context, that is 10^17 times more energy than the largest atomic bomb ever created.
I think that’d probably destroy a city just fine.
P.S. I apologize to any DMs whose players try this in any capacity.




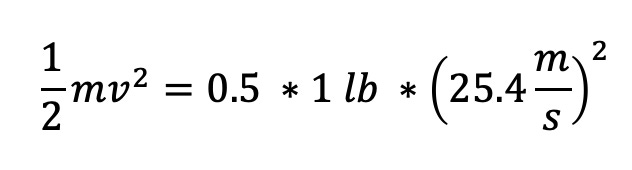






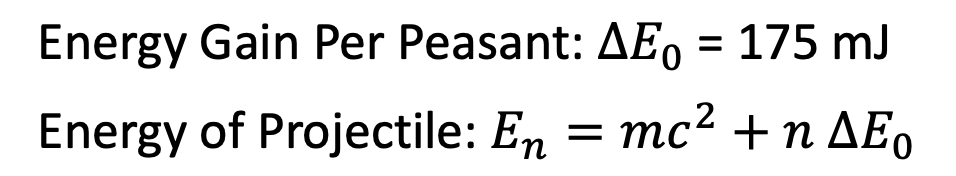


















This is really quite delightful, and I feel like a terrible killjoy for pointing out that your magical nuclear fusion analysis has several problems....
The first is that you haven't really looked at how to heat the rock to T_C. You've calculated the required density needed to get your estimated Coulomb Pressure, assuming the temperature is (somehow) T_C. So how do we go from room-temperature rock to a 3 GK plasma? Rapidly forcing all that rock into a smaller volume *will* heat it up, of course, and maybe you could approximate that as an adiabatic process? (I think the problem might actually be that you pass T_C long before you reach your estimated critical density.)
The second is that silicon burning is *not* actually the fusion of two Si nuclei, so the Coulomb Pressure and critical density calculations are irrelevant. Silicon burning is a complex set of reactions based around the photodissociation of Si (and other) nuclei by gamma rays and subsequent reactions involving the interactions of the protons, neutrons, and alpha particles liberated by the Si (etc.) photodissociation.
(As it happens, the density of a stellar core undergoing silicon burning is more like 10^8 g/cm^3, so you've probably significantly overestimated the number of Enlarge spells needed.)
The third problem is that the plasma will rapidly cool down due to all the photons leaking out through the force wall (it's invisible, after all!), so I suspect that if you *do* get nuclear-burning reactions started, they won't last very long.
And in fact they really won't last very long, because the final problem is that the leakage of thermal photons from a gigakelvin plasma will definitely fry the surroundings, including the spellcasters. Since both spells last only as long as concentration is maintained, the result will be the almost instantaneous vaporization of the casters, followed immediately by the failure of the Wall of Force *and* the Enlarge spells and a (small-ish) blast due to the expanding and cooling hot plasma, which only has as much mass as the original pile of rocks -- though it is very, very hot.
So it's an amusing way of creating a (suicide) bomb, but not one with any meaningful amount of fusion.
This is some great and important work. On the second hypothesis, there’s only one problem as I see it. The way I’ve always played Wall of Force is that spells can’t be cast across it. I.e. they block spell casting. So the stone is never enlarged.